UFF – Física 2 – Provas Antigas – P3 – 2022.1 – Questão 7
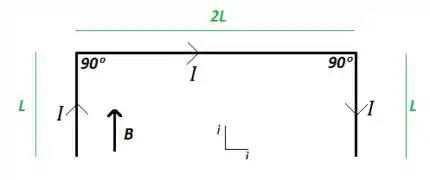
Um fio retilíneo é curvado na forma mostrada na figura abaixo. Determine a força magnética resultante, que atua no fio quando por ele passa uma corrente elétrica , de acordo com o sentido mostrado na figura e na presença de um campo magnético.
A) na direção
B) na direção
C) na direção
D) na direção
E) zero
Passo 1
Eaee!!! Belezinha?
Olha.. basicamente nessa questão temos uma corrente elétrica que percorre um fio, e além disso, estamos na presença de um campo magnético. Se liga no que ta acontecendo:
E a questão nos pede a força magnética resultante nesse trecho, mas como podemos relacionar a força magnética através da corrente elétrica???
Cara, a fórmula da força magnética é esse produto vetorial aqui:
Onde é a corrente, é o comprimento do fio e é o campo magnético. E aí, podemos escrever essa fórmula assim olha:
Onde é o ângulo formado entre a corrente e o campo magnético e é o comprimento do fio.
E aí o que vamos fazer é o seguinte: como o nosso fio tem 3 trechos diferentes, podemos calcular a força magnética em cada um dos trechos, considerando o ângulo , e somar tudo.
Então bora lá!
Passo 2
Pois bem... o fio percorrido pela corrente é submetido a uma força dada por .
Como nos trechos de comprimento o fio é paralelo à corrente, não há presença de força, porque o ângulo entre a corrente e o campo magnético vale . Então olha como fica a força magnética nesses trechos:
Já para o trecho de comprimento , a corrente é perpendicular ao campo magnético, formando um ângulo de . Então, temos que:
Além disso, pela regra da mão direita para o produto vetorial, a força está perpendicular ao papel, saindo dele, ou seja, no sentido de .
Entendeu direitinho? Responde aee ;)
Resposta
B) na direção