UFJF – Física 3 – AV1 – 2017.1 – Questão 2a
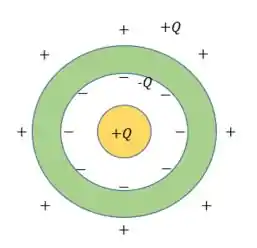
No esquema da figura 1 estão representadas uma esfera compacta de material isolante de raio e uma casca condutora, concêntrica com ela, de raio interno e raio externo . A esfera isolante está carregada uniformemente com densidade volumétrica de carga . A casca condutora tem carga total nula.
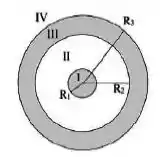
- Qual a carga e como está distribuída nas superfícies interna e externa do condutor?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma esfera isolante dentro de uma casca esférica condutora, as quais estão concêntricas.
A questão nos pede para dizer qual é a carga e sua forma de distribuição das superfícies interna e externa da casca condutora.
E aí? Bora responder?
Passo 2
Bom... primeiramente temos que saber que a carga total da esfera isolante é dada por:
Onde é o volume da esfera e é a densidade de cargas. Assim, temos:
Passo 3
Nesse sentido, como é dito que a carga total da casca condutora é nula, a esfera isolante no interior da casca induzirá uma carga igual a na superfície interna da casca.
Consequentemente, para manter a carga total, uma carga igual a será induzida na superfície externa.
Assim, temos o seguinte esquema:
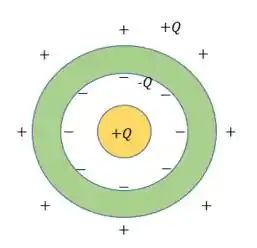
Entendeu direitinho? Responde aee ;)
Resposta
