Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Magnética

Ver Teoria
Exercício 911234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909293949596979899100

Enunciado

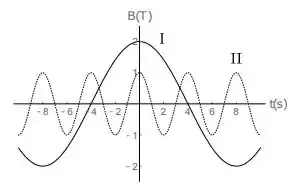
Considere duas situações: na primeira, uma espira circular de área A é atravessada perpendicularmente por um campo magnético uniforme que oscila periodicamente no tempo de acordo com a curva I na figura abaixo (curva cheia), e na segunda situação a mesma espira é atravessada perpendicularmente por um campo magnético uniforme oscilante descrito pela curva II (curva pontilhada). Sejam E I e E I I os valores máximos da força eletromotriz induzida na espira nas situações I e I I , respectivamente. Nessas condições, podemos afirmar que a razão E 1   / E I I vale:

  1. ½
  2. ¼
  3. 1 / 8
  4. 1
  5. 2
  6. 4
  7. 8

Passo 1

Poxa... De acordo com a Lei de Faraday, o módulo da f e m   E (força eletromotriz) pode ser dada pela Lei de Faraday como...

E = d ϕ d t

Onde ϕ representa o fluxo de campo magnético na espira!

Para uma espira quadrada com um campo magnético perpendicular a área da região, esse fluxo é simplesmente o produto do campo pela área A da espira, ou seja...

ϕ = B ⋅ A

Então a primeira coisa que temos que fazer nesse problema é encontrar expressões para o campo magnético B das duas curvas...

E depois calcular a f e m   E   para as duas curvas e compará-los!

Curioso? Então venha comigo !

Passo 2

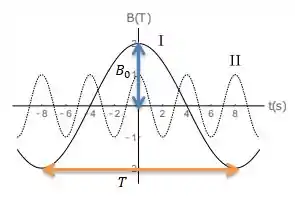
As duas curvas tem um aspecto de curvas cossenoides, logo podemos aferir que o campo magnético B em função do tempo t para cada curva vai ter mais ou menos uma cara assim...

B t = B 0 cos ⁡ ω t

Onde B 0 é a amplitude de cada onda enquanto que ω é a frequência angular da onda dada por...

ω = 2 π T

Onde T representa justamente o período de cada onda, saca?

CURVA I :

Então veja bem, para a primeira curva, a amplitude da onda (valor máximo do campo B ) é no caso igual a 2 Tesla...

B 0 = 2   T

E o período da onda nesse caso é...

T = 16   s

Então...

B I t = 2 cos ⁡ 2 π 16 t   →

B I = 2 cos ⁡ π 8 t  

CURVA I I :

Para a segunda curva (a curva pontilhada), no entanto...

B 0 = 1   T

Enquanto que o período já é...

T = 4   s

Então...

B I I = 1 cos ⁡ 2 π 4 t     →

B I I = cos ⁡ π 2 t

Passo 3

Com os campos encontrados, podemos encontrar o fluxo em cada caso e em seguida derivar com relação ao tempo para determinar a f e m   E ...

CURVA I :

ϕ I = B I ⋅ A   →

ϕ I = 2 cos ⁡ π 8 t ⋅ A

Então a f e m   E I será...

E I = d ϕ I d t     →

E I = 2 A d d t cos ⁡ π 8 t     →

E I = 2 A - π 8 ⋅ sin ⁡ π 8 t     →

E I = - π A 4 sin ⁡ π 8 t

CURVA I I :

No caso da curva I I , o fluxo ϕ I I será...

ϕ I I = B I I ⋅ A   →

ϕ I I = cos ⁡ π 2 t ⋅ A  

E a f e m ...

E I I = d ϕ I I d t     →

E I I = A d d t cos ⁡ π 2 t     →

E I I = A - π 2 ⋅ sin ⁡ π 2 t     →

E I I = - π A 2 sin ⁡ π 2 t

Passo 4

Bem, então considerando apenas o módulo de cada f e m ...

E I = - π A 4 sin ⁡ π 8 t       →             E I = π A 4

E I I = - - π A 2 sin ⁡ π 2 t       →             E I I = π A 2

Então...

E I E I I = π A 4 π A 2 = 1 2

Resposta

Letra A.

Exercícios de Livros Relacionados

Em um modelo pré-mecânica quântica para o átomo de hidrogênio, um elétron orbita em torno de um próton a um raio de 5,29 × 10 - 11m . De acordo com este modelo, qual é a magnitude do campo magnético n
Uma barra metálica de massa m desliza em um par de longos trilhos horizontais condutores, paralelos, separados por uma distância L e conectados a um dispositivo que fornece corrente constante I para o
Um próton está se movendo em uma região onde existe um campo magnético uniforme dado por B → = 10 i ^ – 20 j ^ + 30 k ^ m T . No instante t 1 , o próton possui uma velocidade dada por v → = v x i ^ +
Uma partícula alfa se move com uma velocidade v → de módulo 550 m / s em uma região onde existe um campo magnético B → de módulo 0,045 T . (Uma partícula alfa possui uma carga de + 3,2 × 10 - 19 C e u
Um elétron possui uma velocidade inicial de 12,0 j ^ + 15,0 k ^ k m / s e uma aceleração constante de 2,00 × 10 12 m / s 2 i ^ em uma região na qual existem um campo elétrico e um campo magnético, amb