Uma barra fina (i.e. de espessura desprezível) de vidro na forma de um arco de circunferência de raio (conforme mostra a figura) possui uma carga uniformemente distribuída em seu comprimento.
a) Determine o módulo do campo elétrico no ponto , situado no centro do arco de circunferência.
b) Calcule o campo elétrico no mesmo ponto considerando agora que a carga está distribuída uniformemente ao longo de uma circunferência de raio .
Passo 1
Cara, o campo elétrico de uma cargasinha no ponto tem a seguinte direção...
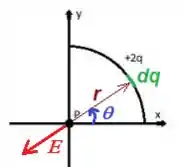
Pela Lei de Coulomb podemos encontrar esse campo elétrico pela fórmula...
Repare que varre toda a carga de até . Então temos que arranjar alguma forma de associar com . E depois integrar em de a cobrindo todo o arco carregado, ta ligado?
Passo 2
POW! Toda vez que você tiver carga distribuída uniformemente, você sempre pode pensar que existe certa quantidade fixa chamada densidade de carga. Ou seja, se estão distribuídos uniformemente em um comprimento , então a densidade vai ser de...
E como é constante para um trechinho pequeno de carga...
Portanto...
Agora quem é ?
Passo 3
Cara, é um comprimentosinho de arco...
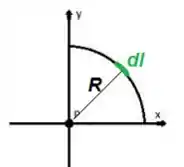
E lembrando-se da Geometria que comprimento de arco sempre pode ser associado com o raio e o ângulo ...
Então...
Passo 4
Pow! Então isso significa que podemos encontrar o campo elétrico através de...
De uma integral! Onde , como já mencionamos varre de a ...
Integrando...
Ta faltando só à informação de ...
Então...
Passo 5
Cara, imagina agora um círculo completinho com essa carga espalhada uniformemente...
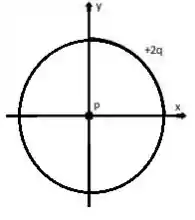
Pow! Imagina o campo criado por um lado...
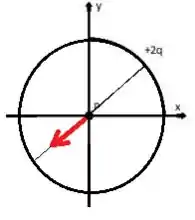
Agora imagina o lado oposto produzindo um mesmo campo elétrico, mas de sentido oposto...
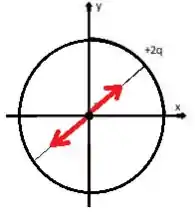
Então no final das contas, o campo total vai zerar quando integrarmos em todo o círculo .
Resposta
LETRA A:
LETRA B: