UFF – Física 2 – Provas Antigas – VR – 2022.1 – Questão 10
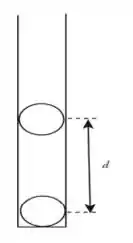
Um tubo de ensaio contém duas bolas de plástico, idênticas e uniformemente carregadas. As bolas estão em equilíbrio e separadas por uma distância , conforme mostrado na figura. Se a carga de cada bola for dobrada, a distância entre as bolas no tubo de ensaio se tornará (o atrito entre as bolas e o tubo pode ser desprezado):
A)
B)
C)
D)
E)
Passo 1
Eaee!!! Belezinha? Olha.. nessa questão a gente quer descobrir o que acontece com a distância quando dobramos a carga de cada bola.
Nesse sentido, sabemos que existe uma força resultante entre as duas bolas que garantem o equilíbrio do sistema. E, falando em força, é interessante lembrar que a força eletrostática é dada por:
Onde é a constante eletrostática, é a carga de uma bola, é a carga da outra bola e é a distância entre elas.
Assim, precisamos comparar essas forças de antes de dobrar a carga e depois de dobrar. Então.. bora lá??
Passo 2
Como já expressamos anteriormente, ao dobrar abas as cargas, as partículas terão que se reorganizar para uma nova distância , de modo a tentar manter a mesma força entre elas, visto que essa garante o equilíbrio do sistema.
Sendo assim, a nova expressão para a força é dada por:
Passo 3
Nesse sentido, igualando as duas forças, temos a nova distância entre as bolas:
Entendeu direitinho? Responde aee ;)
Resposta
B)