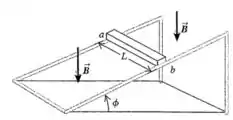
Uma barra metálica de comprimento , massa e resistência total está sobre trilhos metálicos sem atrito, inclinados em um ângulo em relação à horizontal. Os trilhos possuem resistência desprezível. Um campo magnético uniforme de módulo está orientado para baixo, como indicado na figura abaixo. A barra é liberada a partir do repouso e desliza para baixo sobre os trilhos.
d) Depois que a velocidade terminal da barra for atingida, qual será a taxa de conversão de energia elétrica em energia térmica na barra?
e) Depois que a velocidade terminal da barra for atingida, qual é a taxa do trabalho realizado pela força da gravidade? Compare a sua resposta com o que foi encontrado no item (d).
Passo 1
E aí pessoal, tudo bão por aí???
Hoje nós vamos destruir essa questão! Vem comigooo!
O problema aqui é o seguinte, nós temos um trilho inclinado em um ângulo à horizontal na qual desliza para baixo uma barra metálica com massa e comprimento . E a dúvida é: se a barra está sujeita a um campo magnético orientado para baixo, ao deslizar a barra vai atingir a velocidade terminal, nesse caso, qual vai ser a taxa de conversão de energia elétrica em energia térmica e qual a taxa do trabalho realizado pela força da gravidade??
Ihh ferrou, pra descomplicar vamos ter que usar a carta pra resolver no jeitinho do Responde Aí!

Passo 2
d) O enunciado nos pede a taxa de conversão de energia elétrica em térmica, ahhhh mas o que é isso? Basicamente o enunciado está nos pedindo a potência!! Que é expressa pela fórmula seguinte.
Você lembra que no item anterior, nós tínhamos determinado que a corrente induzida equivale a ? Então é só substituir na fórmula da potência!
Prontinho, conseguimos determinar a taxa de conversão de energia!
Passo 3
e) E para finalizarmos, o item e nos pede para descobrirmos a taxa de trabalho exercida pela força da gravidade. Ou seja, a gravidade está exercendo um trabalho ao aplicar uma força para deslocar a barra a uma velocidade , portanto a taxa de trabalho pode ser expressar por:
A força aplicada na barra é aa força resultante quando a força é decomposta, assim como pode ser visto na imagem abaixo.
Logo, . E a velocidade que a barra se desloca nós já tínhamos encontrado no item anterior, logo, . Substituindo esses termos na equação da taxa de trabalho, temos:
E simplificando, teremos:
Ahh e tem um segredinho, você percebeu que a taxa de conversão de energia elétrica em térmica é IGUAL a taxa do trabalho realizado?? Isso faz muuuito sentido se nós pensarmos que o trabalho aplicado para que a barra deslize, atritando ao se deslocar, e assim gerando energia térmica!!
Prontinho, conseguimos uuhhhh!
Curtiu a resolução? Responde Aí!!