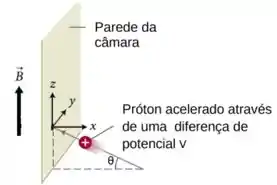
Um próton de massa e carga é acelerado através de uma diferença de potencial , e disparado na direção de uma câmara, como mostrado na figura ao lado. Na figura, a câmara é toda a região à esquerda da parede. Não há campo elétrico na câmara, mas há um campo magnético uniforme na direção positiva. O próton entra na câmara através de um furo na parede, formando um ângulo com o eixo . Considere este ponto de entrada como a origem do sistema de coordenadas . Determine as coordenadas do local, na parede da câmara, que o próton irá atingir, pelo lado de dentro, após interação com o campo magnético. Dica: O próton fará um movimento do tipo espiral dentro da câmara.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um próton que é acelerado por uma tensão e arremessado a uma câmara.
A questão nos pede para dizer quais as coordenadas do local, na parede da câmara, que o próton irá atingir, pelo lado de dentro, após interação com o campo magnético uniforme na direção positiva.
E aí? Como a gente pode resolver? Bora devagarinho aqui!!
Passo 2
Bom... primeiramente vamos determinar a velocidade do próton.
Pela Lei da conservação da energia, toda a energia potencial devido a tensão () se transforma em energia cinética (.
Assim, temos:
Onde é a velocidade, é a carga e é a massa do próton.
Passo 3
Quanto ao movimento do próton, ao atravessar a câmara, verifica-se que surgirá uma força atuando sobre a partícula.
Sobre ela, percebe-se que como a velocidade pertence ao plano , e o campo magnético ao plano , a força magnética, deve ser perpendicular à trajetória, está direcionada inicialmente no sentido positivo de .
Além disso, vale ressaltar que, por ser sempre perpendicular à velocidade do próton, a força magnética atua alterando apenas a sua trajetória, como uma força centrípeta.
Essa característica ocasionaria uma trajetória espiral ao próton.
No entanto, devido a presença da parede, o próton entrará pelo orifício e percorrerá uma trajetória mais semelhante a uma semicircunferência.
Passo 4
Assim, para a força magnética que atua sobre o próton, temos:
Obs: é o ângulo entre a velocidade da partícula e o campo magnético .
Passo 5
Por fim, sabendo que atua como força centrípeta e que o próton percorre uma trajetória aproximadamente semicircular, percebe-se que a distância percorrida pelo próton no plano da parede equivale a duas vezes o raio da trajetória .
Sendo assim, calcula-se o raio:
Portanto, temos que , onde .
Passo 6
Dessa forma, podemos determinar as coordenadas do ponto de chegada:
- : Plano da parede.
- .
- .
Entendeu direitinho? Responde aee ;)
