A figura abaixo ilustra uma partícula que descreve uma trajetória semicircular ao entrar em uma região com campo magnético uniforme.
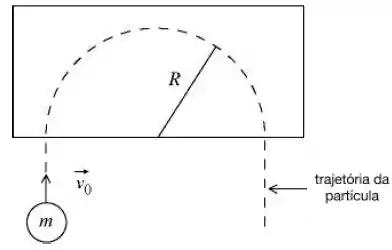
O raio da trajetória é e o módulo da velocidade da partícula ao entrar na região com campo magnético é . Sabendo que a partícula tem massa e carga , qual a magnitude e sentido do campo magnético?
, entrando na folha de papel.
, saindo na folha de papel.
, entrando na folha de papel.
, saindo na folha de papel.
, entrando na folha de papel.
Passo 1
O raio da trajetória é dado por:
Reorganizando os termos:
Substituindo os valores:
Passo 2
Para que a partícula percorra a trajetória circular, é necessário que a força magnética aponte sempre para o centro da trajetória.
A força magnética sobre a partícula é dada por:
Como a carga é negativa, o produto vetorial irá apontar no sentido contrário ao da força, logo:
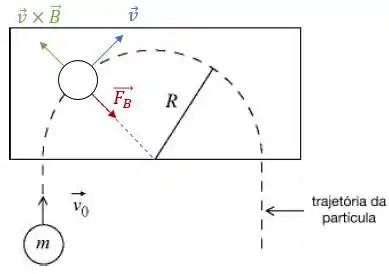
Nesse caso, utilizando a regra da mão direita, onde o dedo indicador tem o mesmo sentido do vetor e o dedo polegar tem o mesmo sentido de , temos que o campo magnético, representado pelo dedo médio, irá apontar para dentro do plano na página.
Assim, a resposta certa é a letra .
Resposta
, entrando na folha de papel.