Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Magnética

Ver Teoria
Exercício 901234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889919293949596979899100

Enunciado

Um campo elétrico E t = k E 0 e α t , onde E 0 , dado em V / m , α , dada e s - 1 são constantes, e t é o tempo em s , é aplicado no interior de uma região cilíndrica de raio R 0 que possui seu eixo de simetria orientado na direção k . Seja r a distância radial ao eixo de simetria da região cilíndrica, r é dado em m .

(a) Calcule o vetor campo magnético B ( r ) para r   >   R 0 .

(b) Calcule o vetor campo magnético B ( r ) para   r   <   R 0 .

Passo 1

Cara... Aqui temos um cilindro de raio R 0 com o eixo em cima do eixo z ...

E aí por esse cilindro a gente faz passar cum campo elétrico na direção do eixo z , como mostra a figura, de modo que ele varie com o tempo t pela equação...

E t = k E 0 e α t

De acordo com a nossa teoria eletromagnética então, quando esse campo E → varia com o tempo, surge ao redor dele um campo magnético concêntrico que depende somente do raio r de distância do eixo do cilindro...

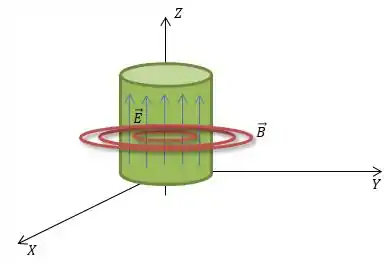
E a gente vai poder encontrar esse campo magnético de acordo com a Lei de Maxwell, para a indução de campo magnético...

∇ × B → = μ 0 ε 0 d E → d t

Passo 2

L e t r a   A :

Queremos nessa Letra A o campo magnético B → para r < R 0 .

Bem, usando a Lei de Maxwell, e sabendo que o campo elétrico E → dentro do cilindro vale... E t = E → = k E 0 e α t Então...

∇ × B → = μ 0 ε 0 d E → d t   →

∇ × B → = μ 0 ε 0 d d t k E 0 e α t   →

Então, derivando...

∇ × B → = μ 0 ε 0 ⋅ k E 0 e α t ⋅ α   →

∇ × B → =   α   μ 0 ε 0 E 0 e α t ⋅ k  

Passo 3

Por outro lado, o rotacional (esse lado esquerdo) pode ser escrito em termos das coordenadas cilíndricas como...

∇ × B → = 1 r ∂ r B ∂ r   ⋅ k  

Claro, isso porque o campo magnético B só depende do raio r de distância do eixo do cilindro, ok? Se não ele seria um vetor gigante, mas aqui nem precisa pensar nisso .

Bem, mas igualando as duas equações...

1 r ∂ r B ∂ r   ⋅ k = α   μ 0 ε 0 E 0 ⋅ k   →

∂ r B ∂ r = α   μ 0 ε 0 E 0 e α t ⋅ r   →

Agora é só resolver essa equação aí! Preparado?

Passo 4

Cara, infelizmente B varia com r , então a gente não pode tirá-lo da derivada, mas ao invés disso, veja que podemos aplicar a regra da produto para derivar esse cara do lado esquerdo...

r ∂ B ∂ r + B ∂ r ∂ r = α   μ 0 ε 0 E 0 e α t ⋅ r   →

r ∂ B ∂ r + B = α   μ 0 ε 0 E 0 e α t ⋅ r   →

∂ B ∂ r + 1 r B = α   μ 0 ε 0 E 0 e α t  

Agora, veja que essa equação (EDO) é de primeira ordem e linear, então para resolvê-la podemos usar a fórmula de EDO linear...

B = 1 I r ∫ I r ⋅ G r   d r + K

Onde...

I r = e ∫ 1 r   d r         e         G r = α   μ 0 ε 0 E 0 e α t

Então...

I r = e ln ⁡ r = r

Ou seja...

B = 1 r ∫ r ⋅ α   μ 0 ε 0 E 0 e α t   d r + K

B = 1 r α   μ 0 ε 0 E 0 e α t ⋅ r 2 2 + K

B = α   μ 0 ε 0 E 0 e α t ⋅ r 2 + K r

Como o campo magnético quando r → 0 tem que ser 0 , concluímos que dentro do cilindro o campo magnético vale...

B = α   μ 0 ε 0 E 0 e α t ⋅ r 2

Passo 5

L e t r a   B :

Esse é então o campo dentro do cilindro. Fora do cilindro, o campo será quase a mesma coisa, mas...

A diferença é de que o r dentro da integral deverá varia de 0 a R 0 ...

B = 1 I r ∫ 0 R 0 I r ⋅ G r   d r

Onde vamos chegar ao valor de...

B = α   μ 0 ε 0 E 0 e α t ⋅ R 0 2 2 r

Resposta

Letra A:

B = α   μ 0 ε 0 E 0 e α t ⋅ r 2

Letra B:

B = α   μ 0 ε 0 E 0 e α t ⋅ R 0 2 2 r

Exercícios de Livros Relacionados

Em um modelo pré-mecânica quântica para o átomo de hidrogênio, um elétron orbita em torno de um próton a um raio de 5,29 × 10 - 11m . De acordo com este modelo, qual é a magnitude do campo magnético n
Uma barra metálica de massa m desliza em um par de longos trilhos horizontais condutores, paralelos, separados por uma distância L e conectados a um dispositivo que fornece corrente constante I para o
Um próton está se movendo em uma região onde existe um campo magnético uniforme dado por B → = 10 i ^ – 20 j ^ + 30 k ^ m T . No instante t 1 , o próton possui uma velocidade dada por v → = v x i ^ +
Uma partícula alfa se move com uma velocidade v → de módulo 550 m / s em uma região onde existe um campo magnético B → de módulo 0,045 T . (Uma partícula alfa possui uma carga de + 3,2 × 10 - 19 C e u
Um elétron possui uma velocidade inicial de 12,0 j ^ + 15,0 k ^ k m / s e uma aceleração constante de 2,00 × 10 12 m / s 2 i ^ em uma região na qual existem um campo elétrico e um campo magnético, amb