Uma partícula de carga elétrica penetra numa região de campo magnético uniforme com uma velocidade . Observe que , e denotam os vetores unitários ao longo dos eixos , e , respectivamente. Sabe-se que a massa da partícula em questão é . Nestas circunstâncias, calcule:
- O vetor força magnética que atua sobre a partícula.
- O cosseno do ângulo formado entre os vetores e .
- O deslocamento da partícula ao longo da direção paralela ao campo magnético quando a mesma completa um período de seu movimento de rotação.
- O raio da trajetória seguida pela partícula.
Passo 1
a) A força magnética atuando sobre uma carga que tem velocidade na presença de um campo magnético é dada por
Como e , teremos que a força será dada por:
Passo 2
b) Para calcular , temos que lembrar que o produto escalar entre dois vetores quaisquer e é dado por
sendo que é o ângulo entre e . Para o caso do nosso problema, teremos
já que e .
Passo 3
c) Vamos supor que a carga esteja, em , no plano da página (plano -), na origem do sistema de coordenadas, como mostra a figura à esquerda abaixo. Nesse caso, o eixo está saindo do plano da página.
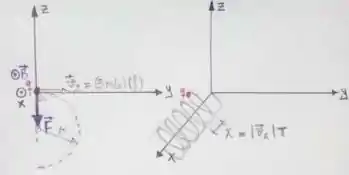
Nesse instante de tempo, no plano -, tem uma velocidade e sobre ela atua uma força , que é perpendicular tanto ao campo magnético , o qual está saindo da página, quanto à . Portanto, no plano -, a carga executa um MCU, com trajetória de raio , como mostrado na figura acima.
No entanto, essa partícula também tem componente da velocidade ao longo da direção e sentido de : . Isso significa que, para , a partícula carregada vai estar saindo do plano da página e cada mais próxima dos nossos olhos. Por isso, a trajetória de será helicoidal: no plano -, um MCU, mas sempre se afastando desse plano em direção aos nossos olhos com velocidade constante , já que em não há força resultante atuando sobre , como está na figura à direita acima.
Portanto, a partícula executa um movimento retilíneo uniforme (MRU) na direção e sentido de . Por isso, como a posição inicial de é (em , ela estava sobre a origem ), a partícula percorre, após um período de sua rotação no MCU, um distância igual a
Agora, como o período é dado por
essa distância será
que é o valor da distância obtido quando a gente substitui os valores do enunciado.
Passo 4
d) O raio da trajetória circular que a descreve no plano - é: