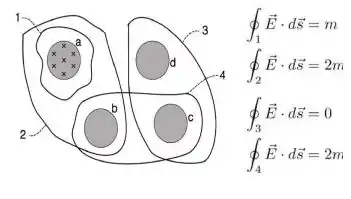
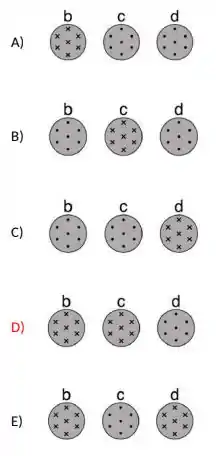
A figura mostra quatro regiões, indicadas pelas letras 'a', 'b', 'c' e 'd', nas quais um campo magnético perpendicular à folha de papel varia no tempo. Nas quatro regiões, o campo magnético aumenta, em módulo, a taxas iguais. A integral de linha do campo elétrico ao longo das quatro curvas fechadas, numeradas de 1 a 4, está expressa em termos de uma constante . Qual alternativa indica corretamente o sentido do campo magnético nas regiões 'b', 'c' e 'd'?
Passo 1
“My God! Que exercício complicado”
Calma jovem gafanhoto! Realmente parece muito difícil, mas na verdade é apenas uma aplicação da teoria da Lei de Faraday que nos diz que em regiões onde se tem variações do fluxo do campo magnético, então terá uma induzida na borda da região (tipo a corda )...
Mas a também pode sempre ser escrita como uma integral de linha...
Onde representa a curva que circula a região de variação de campo magnético. Então...
Mas é claro! Isso só funciona se tiver um fluxo magnético total que varia no tempo, saca? Então o que basicamente a gente vai fazer nesse exercício é olhar para a integral de linha que ele nos deu e concluir sobre o fluxo do campo magnético dentro da curva dada. Assim, a gente vai saber quem é o campo magnético nas bolinhas !
BORA?
Passo 2
Bem... Primeiro, vamos olhar apenas para as duas integrais de linha:
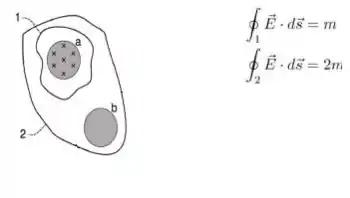
Bem, a primeira integral de linha ao redor da curva é um valor , o que significa que o campo magnético entrando no papel está variando como o enunciado já nos disse.
A integral de linha ao redor da curva é igual a , Isso significa que o campo em deve ter a mesma direção que o campo (para dentro da folha):
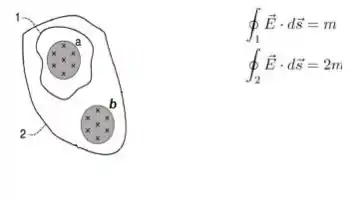
Só assim vamos ter um fluxo total na região variando a : um é devido ao e o segundo devido ao , gerando então , saca?
Passo 3
Agora olhemos também para a Integral...
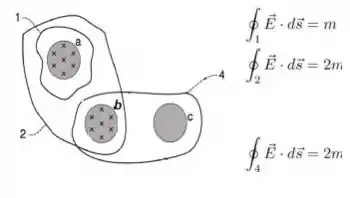
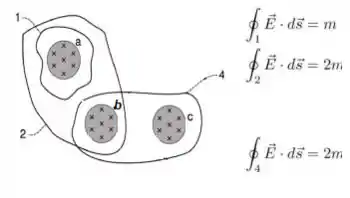
Pelo mesmo motivo que o item anterior, podemos dizer que o campo magnético em tem o sentido apontado para dentro da folha...
Passo 4
Finalmente agora vamos olhar para a última curva que falta..
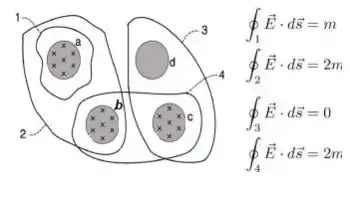
POW! Repare que a integral de linha na curva é igual a . Pela Lei de Faraday então...
O que significa que o fluxo total do campo magnético nessa região é . Isso só vai acontecer se o campo magnético em tiver uma posição contrária ao campo magnético . Ou seja, ao invés de entrar no papel, ele deve sair dele...
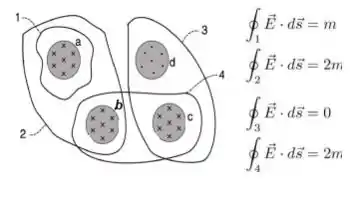
Resposta
Letra D.