. Uma partícula de carga , inicialmente com velocidade , penetra numa região com campo elétrico uniforme e campo magnético uniforme , ambos estacionários, com e . Ao sair desta região, a partícula possui velocidade e está a uma distância de um eixo horizontal, como mostrado na figura abaixo:
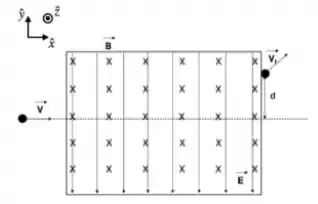
Considere as seguintes afirmativas:
A força que o campo elétrico exerce sobre a partícula realiza trabalho negativo.
Quais destas afirmativas são VERDADEIRAS?
Escolha uma opção:
e
e
e
Nenhuma
e
.
.
Passo 1
Vem comigo que a gente resolve essa juntos!
Nesse problema vamos usar a força elétrica dada por:
E vamos usar também a força magnética, dada por:
Usando essas definições podemos saber para onde cada força dessas que atua na partícula aponta. E com isso vamos saber qual é a maior força já que a partícula foi deslocada para direção que essa força aponta, no caso a direção .
Com isso vamos poder ver quais alternativas são verdadeiras ou falsas.
Passo 2
Vamos analisar as forças primeiro, começando com a elétrica, temos:
Onde , assim:
Então essa força aponta para .
Agora a magnética, temos:
Onde temos e inicialmente temos , assim:
Então temos que:
Então essa força aponta para .
Com isso podemos ver que o módulo da força magnética é maior que o da força elétrica, já que a partícula sofre um deslocamento para direção .
Passo 3
Vamos analisara primeira afirmação.
O trabalho pode ser dado por:
A força elétrica como já vimos ela aponta para e o vetor deslocamento da partícula tem componentes e por conta do deslocamento que ela sofre por conta da força resultante, assim:
Logo esse trabalho feito por essa força é negativo.
Passo 4
Vamos analisar a segunda afirmação.
Nós já vimos no passo que o módulo da força magnética é maior que o módulo da força elétrica, isso quer dizer que:
Logo essa firmação é verdadeira.
Passo 5
Vamos para a última afirmação.
No começo da situação no enunciado a partícula tinha uma velocidade , que tem módulo
Só que quando ela entra na região dos campos ela começa a sofrer uma força resultante na direção , então ela adquire uma aceleração nessa direção que faz com que a partícula ganhe uma velocidade nessa direção, com isso:
E o seu módulo é dado por:
Então se essa velocidade final for igual a inicial, teríamos que:
E isso não faz sentido algum, logo essa afirmação é falsa.
Então só temos a e a como verdadeiras, logo a nossa alternativa vai ser a letra .
Resposta
e