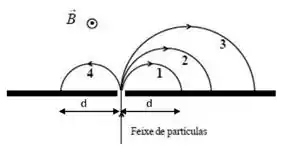
11 - Considere a trajetória das partículas 1, 2, 3 e 4 através de um espectrômetro de massa, conforme a figura. Considere também que todas as partículas entram no espectrômetro com a mesma velocidade e que possuam carga ou . Podemos afirmar que:
Passo 1
O campo magnético do espectrômetro apontado para fora da sua telinha exerce uma força que aponta todo o tempo perpendicular a velocidade das cargas, o que a faz girar com raio .
Podemos encontrar esse raio, verificando então que a força magnética atua como força centrípeta na partícula! Ora, a força magnética de um campo perpendicular à velocidade é dada por:
Já lá da mecânica, força centrípeta é:
Igualando então as duas coisas...
Portanto, quem tiver a maior massa, tem os maiores raios!
Através dessa conclusão, podemos falar que no nosso problema...
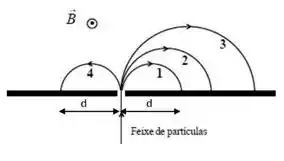
As massas possuem essa ordem aqui:
Passo 2
Agora, temos que verificar com relação às cargas (que está relacionada com a direção do giro).
Pela regra da mão direita, você deve posicionar a sua mão dessa forma aqui:
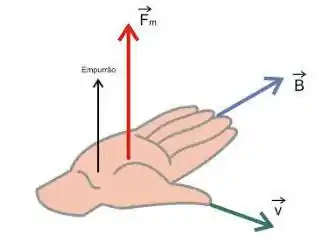
Se a carga for positiva, você empurra na direção que está aí. Já se ela for negativa, você a empurra com o dorso. Saca?
Se você utilizar essa regra aqui:
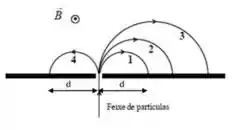
Seus dedos ficarão para cima (saindo da tela do seu PC), enquanto o dedão vai estar na direção do feixe. Então, as cargas que estão na frente da sua mão são positivas e são todas elas: , e . A outra carga estará no dorso e será negativa ().
Resposta
Letra E.