UFJF – Física 3 – AV2 – Questão 3
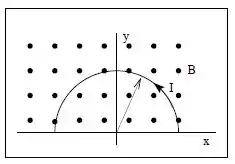
Um fio portador de corrente I está com a forma de uma semicircunferência de raio R, que está no plano . Há um campo magnético uniforme , perpendicular ao plano da espira, conforme a figura ao lado. Calcule a força que atua sobre a espira.
Passo 1
Olá, tudo tranquilo? Bora resolver essa questão?
A ideia aqui é calcular qual a contribuição da força em cada pedacinho de fio, que esse campo magnético vai fazer! Vamos olhar com carinho a figura
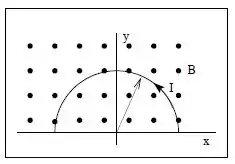
Podemos integrar o elemento de força atuando sobre um elemento de comprimento entre e para encontrar a força atuando sobre a porção semicircular do laço e usar a expressão para a força sobre um fio portador de corrente em um campo magnético uniforme para encontrar a força sobre o segmento reto do laço.
Assim a força total vai ser a soma das duas partes:
Mas você lembra como encontrar essa força?
Se o caminho for constante (no caso do fio reto)
Agora quando o fio é curvo, precisamos integrar!
Então é isso! A ideia aqui é aplicar essas fórmulas para cada situação (usando e abusando da simetria no fio circular) e somar as contribuições!
Mas pode ficar tranquilo, vou fazer passo a passo com você!
Vamos começar?
Passo 2
Vamos começar pelo fio curvo! Dá uma olhada com carinho nessa figura aqui
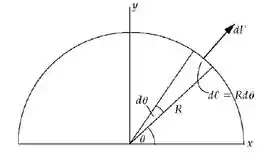
Certo! Temos que expressar a força atuando no fio de comprimento :
Expressando agora as componentes e de
Assim nossa única componente é :
Resolvendo, temos
Assim a força magnética nessa parte circular do fio aponta para cima! Tranquilo? Vamos para o cálculo da parte reta!
Passo 3
Agora expressando a força atuando no laço do segmento reto, temos:
Como o comprimento está sempre na mesma direção do campo, tudo é constante e podemos apenas calcular!
Beleza? Agora só falta somar as duas parcelas da força!
Passo 4
Agora nossa missão é somar as duas contribuições:
Gente, eles tem módulos iguais!
assim a força total é zero!
Ufa, terminamos! #partiu treinar mais?