Em um espectrômetro de massa, um feixe de íons emitido por uma fonte atravessa uma região de campo magnético uniforme e estacionário, como mostrado na figura abaixo.
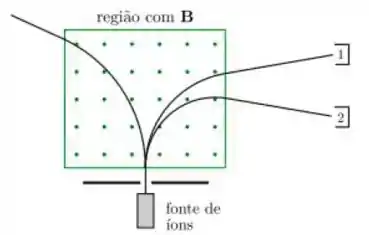
Esse sistema é utilizado para determinar a quantidade de água pesada (, onde representa um átomo de deutério) que há na água do mar. Como resultado da ionização, separa-se apenas os íons , e , que são então acelerados de forma a entrar na região de campo magnético com a mesma velocidade inicial. Sabendo que as massas dos átomos de , e valem 1, 2 e 16 u.m.a, respectivamente, e que a massa do elétron pode ser desprezada em confronto com as massas do próton e do nêutron, podemos afirmar que os íons coletados nos detectores 1 e 2, respectivamente,
- e
- e
- e
- e
- e
Passo 1
Para começar a conversa aqui, o que a gente tem são partículas carregadas com cargas diferentes, com velocidade iguais entrando em uma mesma região onde tem um campo magnético uniforme e estacionário, ou seja, esse campo tem o mesmo valor em todos os pontos da região (uniforme) e não varia à medida que o tempo passa (estacionário).
Antes, precisamos nos lembrar que, cada uma dessas cargas vai sentir uma força que é dada por:
Para o nosso problema, cada uma cargas que vamos analisar tem módulos e sinais diferentes: e tem carga de mesmo módulo e mesmo sinal, porém massas diferentes; tem carga negativa, com dobro do módulo das outras duas cargas.
Características importantes que estão nessa expressão:
- tem a mesma direção do vetor ;
- é sempre perpendicular tanto a quanto a ;
- não muda o módulo , mudando apenas a direção da velocidade de ;
- tem a mesma direção e sentido do vetor se ;
- tem a mesma direção e sentido contrário do vetor se .
Passo 2
Agora, vamos olhar para essas características de junto com vetores desenhados na figura abaixo. Quando as partículas estão no ponto de entrada da região de , a velocidade está apontando para cima e tem o mesmo valor para todas as cargas. Por isso, o vetor , como mostra a figura abaixo, está apontando da esquerda para a direita perpendicular a e e esse produto vetorial é independente do sinal das cargas, ok?
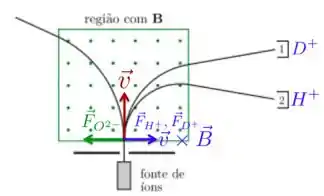
Para as cargas positivas e , a força estará na direção e sentido do vetor e também terá a mesma intensidade para as duas. Agora a força sobre a carga negativa terá mesma direção , porém com sentido contrário, apontando da direita para a esquerda, como está na figura acima.
Com isso, a gente já sabe quais cargas vão para a direita e atingirão os detectores: e . Só precisamos saber agora qual o detector cada uma dessas cargas positivas atinge.
Passo 3
Para fechar a conversa aqui, vamos usar as características 2 e 3 de que a gente listou lá no Passo 1. Essa força é sempre perpendicular a velocidade das cargas, por isso não muda a intensidade das cargas. Porém, muda a direção do vetor velocidade , acelerando essas partículas carregadas e sempre está direcionada para o centro da trajetória de , ou seja, é uma força centrípeta.
Essas são características lá o Movimento Circular Uniforme (MCU). As partículas vão descrever, então, órbitas circulares dentro de , cujo raio será:
No caso das cargas e , que têm mesmos e , a que tiver maior massa descreverá a órbita com maior raio e atingirá o detector 1. Por essa razão, atinge o detector 1 e o detector 2.
Resposta
Letra a.