UFJF – Física 3 – AV1 – 2017.1 – Questão 2b
No esquema da figura 1 estão representadas uma esfera compacta de material isolante de raio e uma casca condutora, concêntrica com ela, de raio interno e raio externo . A esfera isolante está carregada uniformemente com densidade volumétrica de carga . A casca condutora tem carga total nula.
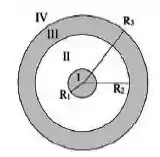
- Calcule o vetor campo elétrico nas regiões .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma esfera isolante dentro de uma casca esférica condutora, as quais estão concêntricas.
A questão nos pede para dizer qual é o vetor campo elétrico nas regiões .
Para isso, é interessante sabermos da Lei de Gauss:
Onde é o campo elétrico, é o diferencial de área da gaussiana, é a carga envolvida e é a constante de permissividade elétrica no vácuo.
E aí? Bora responder?
Passo 2
Bom... primeiramente para a região , onde .
Desenhando uma gaussiana esférica concêntrica com o isolante, temos que o campo elétrico é dado por:
Passo 3
Para a região , temos que, colocando a gaussiana externa ao isolante e interna ao condutor:
Onde é a carga total.
Passo 4
Para a região :
Esta região está localizada exatamente no interior da casca condutora.
Por definição, dentro de um condutor, não existe campo elétrico quando está em situação de equilíbrio eletrostático.
Dessa forma, temos que .
Passo 5
Para a região :
Nessa região, externa a todo o conjunto, a Lei de Gauss relacionará a carga interna de forma semelhante à segunda região.
Isso ocorre porque a gaussiana está no vácuo e engloba toda a carga da esfera.
Dessa forma, temos que:
Entendeu direitinho? Responde aee ;)
Resposta
Região :
Região :
Região :
Região :