Na figura abaixo, uma carga elétrica pontual , de massa , desloca-se ao longo do eixo com uma velocidade constante de módulo . Na origem do sistema de coordenadas (ponto ), tal partícula penetra numa região retangular de largura , onde existe um campo magnético uniforme que é perpendicular ao plano e que “entra” neste plano. Considere que o campo magnético é nulo fora da região indicada na figura. Depois de percorrer tal região de campo magnético, a partícula a abandona no ponto , localizado a uma altura em relação ao eixo . Nestas condições:
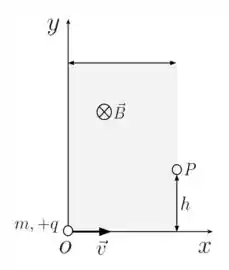
(a) Determine o vetor força magnética (em módulo, direção e sentido) que atua na partícula no ponto .
(b) Sabendo que a partícula entra na região de campo magnético em e sai em , calcule o módulo da velocidade para que isso aconteça, expressando-o em termos de , , , e .
(c) As energias cinéticas da partícula em e são dadas respectivamente por e . Determine .
Passo 1
A direção e o sentido do vetor força magnética pode ser calculado a partir da regra da mão direita. Vamos lá:
- A velocidade aponta para a direita, no sentido crescente da direção do eixo ;
- O campo “entra” no papel, ou seja, no sentido decrescente da direção do eixo ;
- Como a carga é positiva, a força irá apontar para cima, no sentido crescente da direção do eixo .
Beleza?
Passo 2
Para calcular seu módulo, utilizamos a fórmula:
já que e são ortogonais!
Assim, o vetor força magnética será dado por:
Passo 3
A partícula, ao entrar na região cinza, irá percorrer uma trajetória circular. Assim sendo, a força magnética irá funcionar como uma força centrípeta. Ou seja,
onde é o raio da trajetória circular.
Reorganizando a expressão acima, temos:
Passo 4
Temos , e . Precisamos, então, determinar o valor do raio . Para isso, vamos olhar para a figura a seguir. O círculo mostra a trajetória que seria percorrida pela partícula caso houvesse campo magnético em todo o plano .
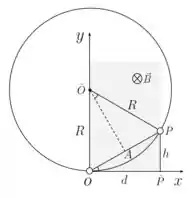
Vamos analisar os triângulos desenhados:
- Os ângulos dos triângulos e marcados são idênticos;
- Ambos os triângulos possuem um ângulo reto;
- Logo, o terceiro ângulo dos dois triângulos também é o mesmo!
- Assim sendo, os triângulos e são semelhantes.
Por semelhança de triângulos, podemos chegar na seguinte expressão:
Mas e quanto vale ?
Passo 5
Sabemos que o triângulo é retângulo e, portanto:
Substituindo na expressão encontrada para , temos:
Passo 6
Temos, finalmente, que o módulo da velocidade é dado por:
Passo 7
A força magnética não realiza trabalho e, como o trabalho realizado sobre um corpo é igual à sua variação da energia cinética,
Resposta
(a) .
(b) .
(c) .