A figura abaixo mostra duas partículas carregadas, 1 e 2, que estão fixas sobre o eixo . O módulo da carga da partícula 1 é , onde é a carga elementar. A partícula 3, de carga , pode ser movida na parte positiva do eixo . O gráfico abaixo mostra a componente da força eletrostática resultante sobre a partícula 2, em função da posição da partícula 3 no eixo. A escala do eixo é dada por . A curva possui uma assíntota para . Use
a) (1,0 ponto) Determine o sinal da carga . JUSTIFIQUE SUA RESPOSTA!
b) (1,5 pontos) Calcule o valor da carga em função da carga elementar . Sugestão: Calcule tudo em função da carga elementar .
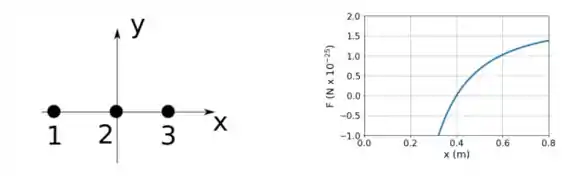
Passo 1
Cara! Observe que a única carga que possui o sinal conhecido é a carga , uma carga positiva. A carga a gente sabe que tem módulo igual a , mesmo módulo da carga 3, mas não sabemos se ela é uma carga positiva ou negativa.
“AH! Então como a gente vai descobrir o sinal da carga?”
Então, olhando para a curva da força resultante em cima da carga 2. Repare que quando a partícula 3 está bem próximo da partícula 2, a força é negativa o que significa que significa que ela apontará no sentido negativo de :
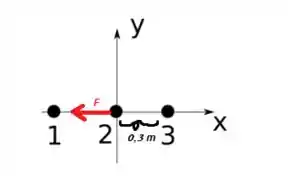
ORA! Isso significa que as partículas 2 e 3 se repelem. E se elas se repelem, é porque possuem o mesmo sinal de carga .
Conclusão: A carga 2 precisa ser positiva.
Passo 2
Cara, sabemos pela Lei de Coulomb que a força em uma carga por uma carga pode ser encontrada por...
E olha que maneiro, o problema nos disse que quando a carga está no infinito () a força presente na carga é dada pelo valor da assíntota (valor quando é muito grande)...
Então, basicamente, podemos conhecer o valor da carga fazendo a substituição...
E repare que a gente conhece a carga e também conhece , falta conhecer , neh? Vamos fazer isso em outro passo então!
Passo 3
é a distância entre a carga e ...
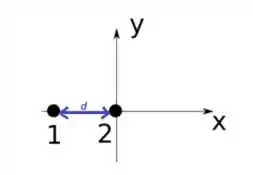
Repare que eu já tirei a carga dali porque a gente está considerando ela no infinito.
Esse valor de não foi nos dado no enunciado. Mas, contudo, não obstante... Tem como da gente descobrir!
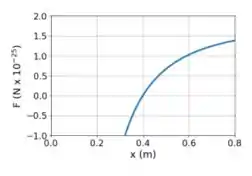
Repare no gráfico que a força quando a carga está em . Para a força em zerar e preciso que a força feita pelas duas cargas adjacente ( e ) seja igual em módulo. E pow... Pensa comigo, se as duas cargas e tem o mesmo módulo, elas só vão conseguir zerar a força na carga se elas estiverem a mesma distância da carga . Isto é, isso significa que a distância da carga até a carga só pode ser !
Passo 4
Descoberto o valor de , podemos voltar para a expressão que determina o módulo da carga ...
POW, simplificando essas continhas...
PRONTINHO! Esse é o valor da carga .
Resposta
LETRA A: Positiva
LETRA B: