Listas de Ondas - UFMG de Fundamentos de Oscilações e Ondas da UFMG - Problemas sobre Oscilador Harmônico
Fundamentos de Oscilações e Ondas - UFMG
Um objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
- A equação do movimento pode ser dada por
Um objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
b) A velocidade máxima do objeto é:
Ver solução completaUm objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
c) A aceleração máxima do objeto é dada por:
Ver solução completaUm objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
d)A energia total do sistema pode ser dada por:
Ver solução completaUm oscilador harmônico simples pode ser descrito pela seguinte equação diferencial: . Considere as seguintes equações abaixo, onde A, e são constantes, e verifique se elas descrevem um movimento MHS.
a )
b)
c)
Ver solução completaUm oscilador harmônico possui frequência e amplitude A.
a )Quais são os valores (módulos) da posição e da velocidade quando a energia potencial elástica for igual a energia cinética?
Ver solução completaUm oscilador harmônico possui frequência e amplitude A.
b)Quantas vezes isso ocorre em cada ciclo e qual é o intervalo de tempo entre duas ocorrências consecutivas?
Ver solução completaUm oscilador harmônico possui frequência e amplitude A.
c)Quando o deslocamento é a metade da amplitude, quais os valores das frações de energia cinética e energia potencial?
Ver solução completaUm certo pêndulo simples possui na Terra um período igual a 1,60 s. Qual é o período na superfície de Marte?
Ver solução completaQuando deslocados da posição de equilíbrio, os dois átomos da molécula de são submetidos a uma força restauradora do tipo F = - kx com a constante k = 580 N/m. Calcule a frequência de oscilação da molécula de . Obs: busque na literatura os dados que você precisará usar para resolver o problema.
Ver solução completaUma pessoa cuja massa é de 60,0 kg executa um salto de Bungee Jump com uma corda elástica de comprimento natural de 9,00 m. Quando ele atinge a parte mais baixa, a corda sofreu uma distensão de 18,0 m e ele se encontra a 3,00 m do solo.
- Calcule a constante-de-mola dessa corda.
Uma pessoa cuja massa é de 60,0 kg executa um salto de Bungee Jump com uma corda elástica de comprimento natural de 9,00 m. Quando ele atinge a parte mais baixa, a corda sofreu uma distensão de 18,0 m e ele se encontra a 3,00 m do solo.
b. Qual é a força máxima exercida sobre a pessoa?
Ver solução completaO problema do “Bungee Jump”
Uma pessoa cuja massa é de executa um salto de Bungee Jump com uma corda elástica de comprimento natural de . Quando ele atinge a parte mais baixa, a corda sofreu uma distensão de e ele se encontra a do solo.
Qual é a aceleração máxima sofrida pela pessoa?
Ver solução completaO problema do “Bungee Jump”
Uma pessoa cuja massa é de executa um salto de Bungee Jump com uma corda elástica de comprimento natural de . Quando ele atinge a parte mais baixa, a corda sofreu uma distensão de e ele se encontra a do solo.
Depois de chegar à parte mais baixa do salto a pessoa tende a oscilar. Calcule a frequência de oscilação considerando que o movimento fosse do tipo .
Ver solução completaO problema do “Bungee Jump”
Uma pessoa cuja massa é de executa um salto de Bungee Jump com uma corda elástica de comprimento natural de . Quando ele atinge a parte mais baixa, a corda sofreu uma distensão de e ele se encontra a do solo.
Normalmente em saltos de Bungee Jump observa-se uma constante de amortecimento da ordem de . Considerando esse valor, calcule a frequência e o período da oscilação sofrida pelo nosso saltador.
Ver solução completaO problema do “Bungee Jump”
Uma pessoa cuja massa é de executa um salto de Bungee Jump com uma corda elástica de comprimento natural de . Quando ele atinge a parte mais baixa, a corda sofreu uma distensão de e ele se encontra a do solo.
Seria possível fazer uma estimativa do tempo em que o indivíduo ficaria oscilando? Explique
Ver solução completaO problema do “Bungee Jump”
Uma pessoa cuja massa é de executa um salto de Bungee Jump com uma corda elástica de comprimento natural de . Quando ele atinge a parte mais baixa, a corda sofreu uma distensão de e ele se encontra a do solo.
Considere agora, que uma outra pessoa (adepta ao consumo farto de massas, chocolates, doces, cerveja, etc…) pesando , inadvertidamente toma da mesma corda e tenta pular!! Supondo que a corda e os cintos resistam ao seu peso, analise com cuidado se essa pessoa correrá algum risco no seu salto.
Ver solução completaAtravés de uma força de , um oscilador harmônico amortecido é deslocado de da sua posição de equilíbrio. Em ele é solto (do repouso) e começa a oscilar. O movimento é então registrado como mostrado no gráfico abaixo. Faça uma estimativa, mais precisa que você conseguir, dos valores do período e da massa.
Um objeto que executa um movimento harmônico simples leva para se deslocar de um ponto de velocidade nula para o ponto seguinte do mesmo tipo. A distância entre os pontos é de . Calcule o período, a frequência e a amplitude do movimento.
Ver solução completaA função descreve o movimento harmônico simples de um corpo. No instante , determine o deslocamento, a velocidade, a aceleração e a fase do movimento. Qual é a frequência e qual o período do movimento?
Ver solução completaUm oscilador é formado por um bloco com uma massa de ligado a uma mola. Quando é posto em oscilação com uma amplitude de , o oscilador repete o movimento a cada . Determine o período, a frequência, a frequência angular, a constante elástica, a velocidade máxima e o módulo da força máxima que a mola exerce sobre o bloco.
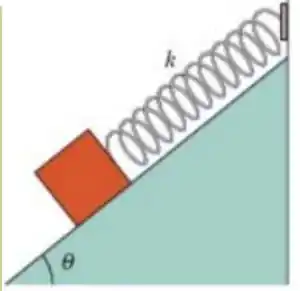
Ver solução completaA figura ao lado mostra um bloco com de peso, que pode deslizar sem atrito em um plano inclinado de ângulo e está ligado ao alto do plano inclinado por uma mola, de massa desprezível, de de comprimento quando relaxada, cuja constante elástica é . A que distância do alto do plano inclinado fica o ponto de equilíbrio do bloco? Se o bloco é puxado ligeiramente para baixo ao longo do plano inclinado e depois liberado, qual é o período das oscilações resultantes?
Um objeto de que repousa em uma superfície horizontal sem atrito está preso a uma mola com . Objeto é deslocado horizontalmente a partir da posição de equilíbrio e recebe uma velocidade inicial de na direção da posição de equilíbrio. Determine a frequência do movimento, a energia potencial inicial do sistema massa-mola, a energia cinética inicial e a amplitude do movimento.
Ver solução completaDetermine a energia mecânica de um sistema bloco-mola com uma constante elástica de e uma amplitude de oscilação de .
Ver solução completaUma partícula de executa um MHS com uma amplitude de , uma aceleração máxima de módulo e uma constante de fase desconhecida . Determine o período do movimento a velocidade máxima da partícula e a energia mecânica total do oscilador. Qual é o módulo da força que age sobre a partícula no ponto no qual o deslocamento é máximo? O deslocamento é metade do deslocamento máximo?
Ver solução completaUma mola, de massa desprezível, está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição tal que a mola se encontra no estado relaxado. Em seguida, o objeto é liberado e passa a oscilar para cima e para baixo, com a posição mais baixa abaixo de . Qual a frequência das oscilações? Qual é a velocidade do objeto quando se encontra abaixo da posição inicial? Um objeto de massa é preso ao primeiro objeto, após o que o sistema passa a oscilar com metade da frequência original. Qual é a massa do primeiro objeto? A que distância abaixo de está a nova posição de equilíbrio (repouso), com dois objetos presos à mola?
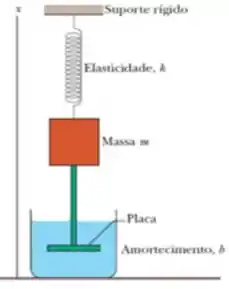
Ver solução completaEm um oscilador amortecido como o que está mostrado na figura ao lado, o bloco possui uma massa de e a constante elástica é . A força de amortecimento é dada por , em que . O bloco é puxado para baixo e liberado. Calcule o tempo necessário para que a amplitude das oscilações resultantes diminua para um terço do valor inicial. Quantas oscilações o bloco realiza neste intervalo de tempo?
A amplitude de um oscilador fracamente amortecido diminui de a cada ciclo. Que porcentagem da energia mecânica do oscilador é perdida em cada ciclo?
Ver solução completaEm um circuito oscilante com e , considere que a corrente inicial seja máxima. Calcule o tempo necessário para o capacitor carregar completamente pela primeira vez.
Ver solução completaConsidere um circuito LRC em série onde . O capacitor é carregado com uma carga inicial e então o circuito é colocado para oscilar. Sabendo-se que o período da oscilação não amortecida é de e o coeficiente de amortecimento é , pede-se:
Escreva a equação da oscilação dom todas as constantes numéricas.
Calcule os valores da capacitância e da resistência.
Ver solução completaUma esfera sólida de raio flutua, em repouso, em um líquido cuja densidade é com a metade de seu volume submerso. Quando a esfera é suavemente empurrada para baixo e então solta ela começa a oscilar harmonicamente . Mostre que, para estas condições, a frequência de oscilação pode ser calculada por:
onde é a aceleração da gravidade.
Ver solução completaConsidere que você queira construir um circuito para oscilar na frequência de e você tem um indutor de Qual o valor da capacitância você deverá usar? Se o capacitor é inicialmente carregado até qual a carga de pico (máxima) no capacitor? Qual é a energia total no circuito?
Ver solução completaUm pêndulo constituído de uma esfera presa a um fio de comprimento é solto de uma posição , a partir do repouso. Considerando a aproximação para a validade do movimento harmônico simples mostre que a velocidade do pêndulo ao passar por pode ser calculada por . Usando a conservação da energia encontre essa velocidade exatamente para um ângulo qualquer (não somente para pequeno ângulo!!) e mostre que seu resultado está de acordo com o resultado do item quando for pequeno. Encontre a diferença entre o valor aproximado e o valor exato para e . Encontre a diferença ente o valor aproximado e o valor exato para e . Compare os resultados dos itens e . O que você conclui?
Ver solução completaSobre a superfície muito lisa de uma mesa se encontra uma mola, cuja a constante é de . Uma das extremidades da mola está fixada na mesa e na outra está presa um bloco de que também repousa sobre a mesa. Um outro bloco (também de ) desloca sobre a superfície com velocidade de e colide com o bloco preso à mola. Após a colisão, os dois blocos permanecem grudados um no outro e o sistema começa a oscilar. Considerando e no instante da colisão, encontre a equação do movimento harmônico resultante.
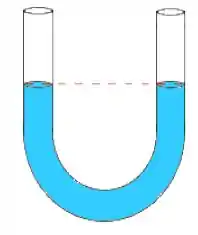
Ver solução completaUm tubo de secção transversal é dobrado na forma de um . Um fluído é inserido no tubo ocupando um comprimento do tubo. O fluido é sugado de um lado do tubo e então é solto, resultando em um movimento oscilatório (considere que não tem atrito).
Mostre que o período de oscilação do movimento harmônico resultante é dado por:
Um pêndulo de de comprimento é deslocado lateralmente até um ângulo de e então é liberado.
Quanto tempo leva o peso do pêndulo para atingir a velocidade mais elevada?
Ver solução completaUm pêndulo de de comprimento é deslocado lateralmente até um ângulo de e então é liberado.
Quanto tempo levaria se o pêndulo fosse liberado em um ângulo de ?
Ver solução completaUm peso desconhecido é preso a uma das extremidades de uma mola e prova uma elongação da mola de uma distância , na posição de equilíbrio. Mostre que, nestas condições, se o peso for colocado para oscilar em MHS, o período é o mesmo de um pêndulo simples de comprimento .
(Obs: considere a mola de massa desprezível).
Ver solução completaMostre que para um oscilador harmônico amortecido, sob a ação de uma força do tipo , oscilações ocorrerão somente quando for satisfeita a condição .
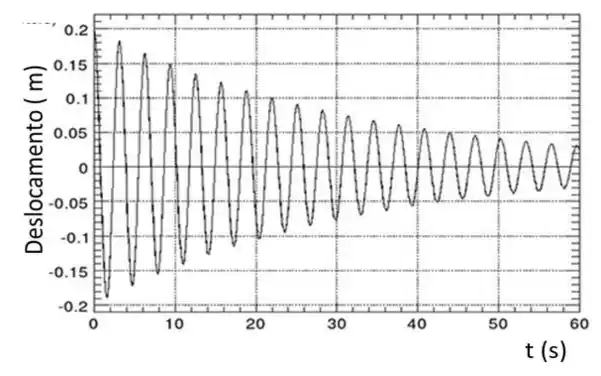
Ver solução completaO gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
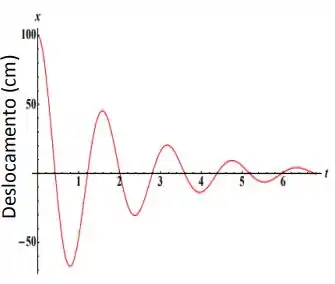
Usando as informações do gráfico faça uma estimativa dos valores da frequência de oscilação e do coeficiente de amortecimento .
(Dica: se necessário amplie a figura)
Ver solução completaO gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
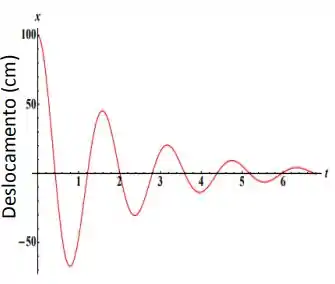
Determine a frequência natural do MHS.
Ver solução completaO gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
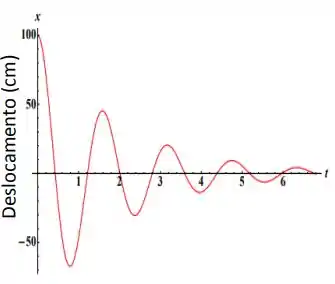
Determine o período de oscilação do oscilador amortecido.
Ver solução completaO gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
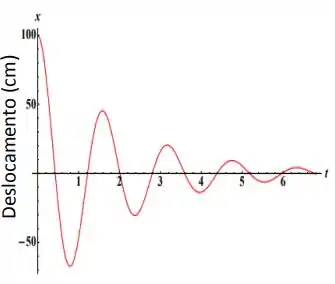
Escreva a equação para o oscilador amortecido.
Ver solução completaA figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
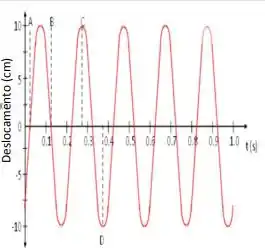
a. A constante de fase () do movimento.
Ver solução completaA figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
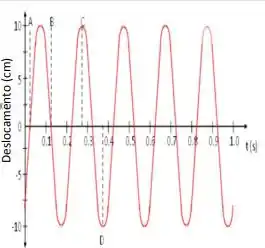
b. Escreva a equação do deslocamento em função do tempo.
Ver solução completaA figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
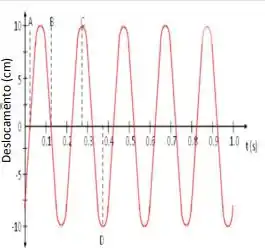
c. Qual a constante de mola?
Ver solução completaA figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
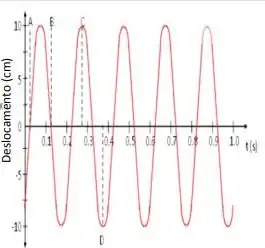
d. Calcule a velocidade máxima.
Ver solução completaA figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
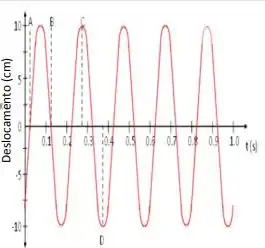
e. Calcule a aceleração máxima.
Ver solução completaA figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
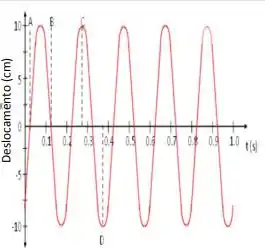
f. Quando exatamente o corpo estará na posição de equilíbrio mas movendo-se para a direita?
Ver solução completaA figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
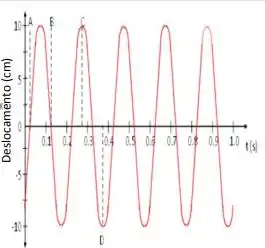
g. Onde exatamente se encontra o corpo no momento correspondente ao ponto C?
Ver solução completaUm bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A velocidade do bloco no instante que ele atinge a mola.
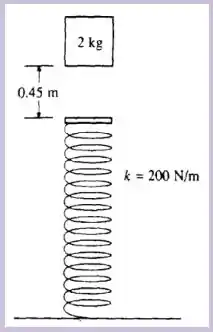
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A força na mola quando o bloco atinge a posição de equilíbrio.
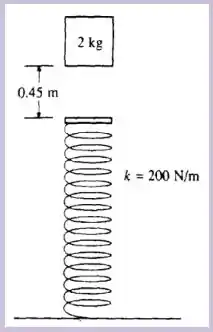
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A distância comprimida da mola na posição de equilíbrio.
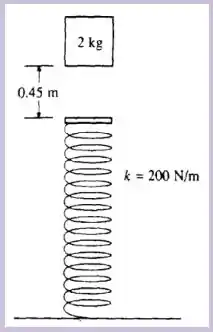
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A velocidade do bloco na posição de equilíbrio.
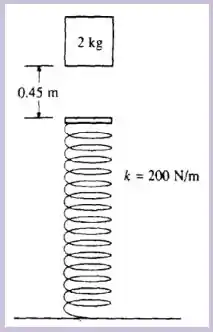
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A amplitude da oscilação resultante
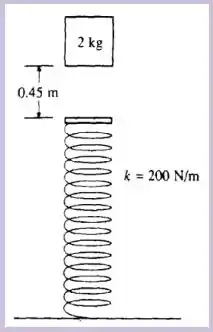
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
O período da oscilação.
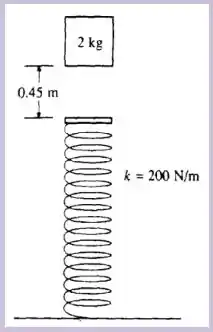
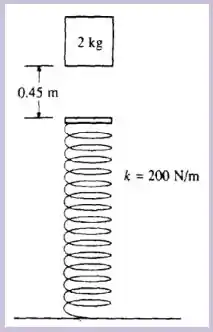
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
Pode-se afirmar que a velocidade do bloco na posição de equilíbrio corresponde a sua máxima? Explique
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
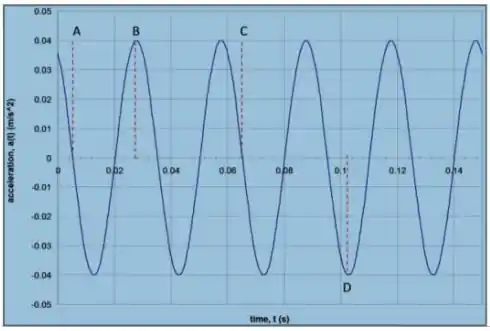
O deslocamento máximo do corpo.
Ver solução completaO gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
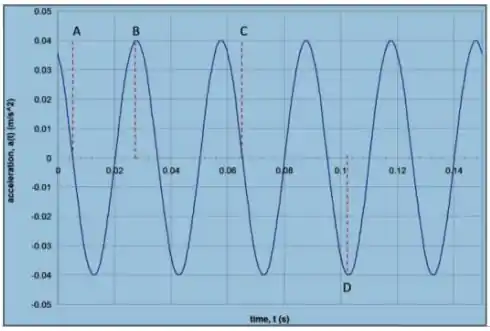
A velocidade máxima do corpo.
Ver solução completaO gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
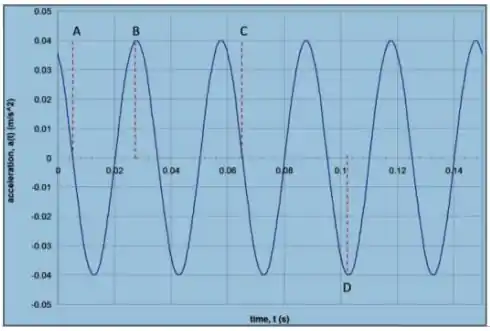
A constante de fase do movimento.
Ver solução completaO gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
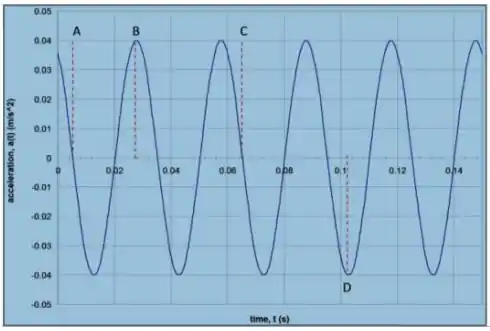
A constante elástica da mola.
Ver solução completaO gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
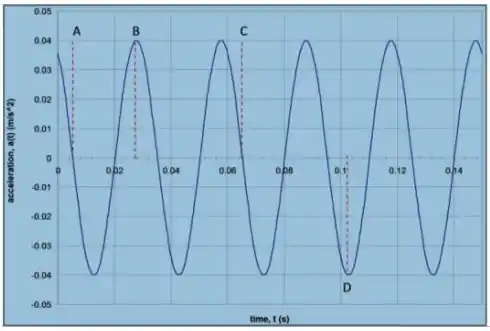
A constante elástica da mola.
Ver solução completaNa figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
a. A velocidade do disco ao passar pela posição de equilíbrio.
Ver solução completaNa figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
b. A frequência angular do movimento.
Ver solução completaNa figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
c. Qual seria a constante elástica para que um sistema consistindo de uma mola e um bloco oscilasse com a mesma frequência que o sistema disco-mola?
Ver solução completaNa figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
d. Qual seria a massa do disco para que a frequência fosse igual a do sistema simples massa-bloco ( com massa M e constante k).
Ver solução completaUm objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
a. Determine a amplitude, a frequência, a frequência angular e o período desse movimento.
Ver solução completaUm objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
b. Escreva a equação da velocidade do objeto.
Ver solução completaUm objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
c. Escreva a equação da aceleração do objeto.
Ver solução completaUm objeto de massa tem um movimento no qual sua posição é descrita pela função onde a distância é medida em metros e o tempo em segundos.
d. Qual o valor da constante-de-mola associada a esse movimento?
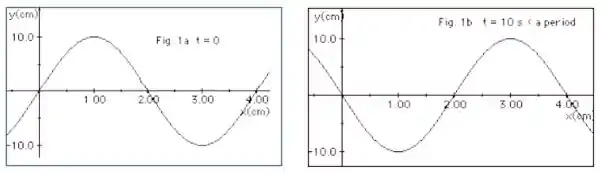
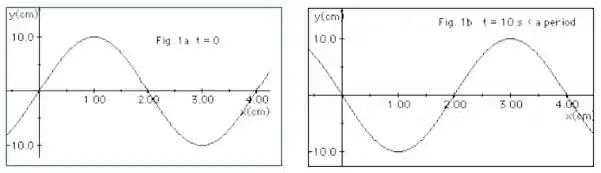
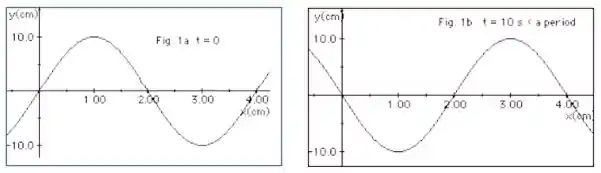
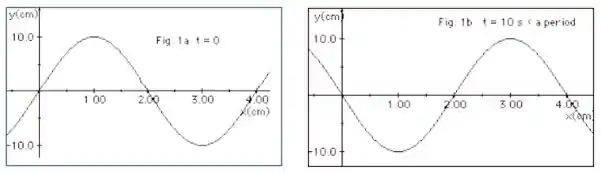
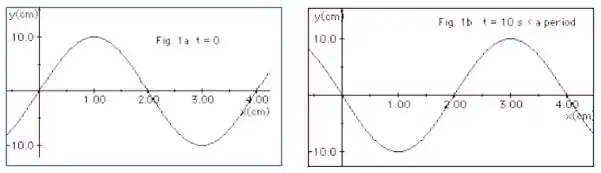
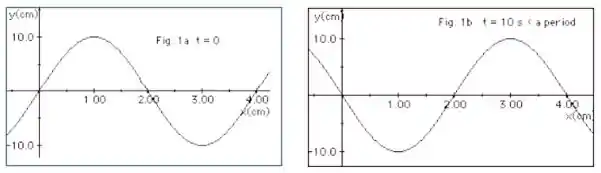
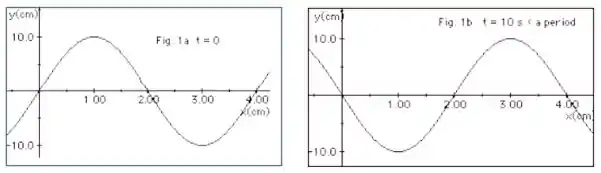
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
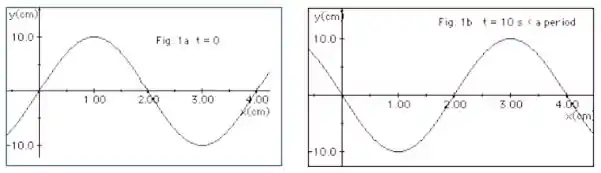
a. O comprimento de onda, a frequência e a velocidade da onda.
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
b. Nesse tempo , determine, à direita no eixo x, as duas próximas posições onde ocorrerão cristas.
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
c. Em que instante posterior ocorrerá outra crista na posição ?
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
d. O número de vezes, no tempo de um período, que o deslocamento da corda é nulo na posição x = 2,0 cm.
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
e. O número de cristas que passam em x = 1,0 cm no tempo de 80 s.
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
f. Desenhe, em um gráfico, o comportamento do deslocamento y em função do tempo para as posições x = 0, x = 2 cm e x = 4,0 cm, para o intervalo de t = 0 até t= 20 s.
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
g. O ponto x = 0 da corda está em fase com os pontos x = 2,0 cm e x = 4,0 cm? Explique.
Ver solução completaA Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
h. Escreva uma função que seja apropriada para descrever o deslocamento y dos pontos da corda para quaisquer valores de x e de t.
Ver solução completa