UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 32f
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
O período da oscilação.
Passo 1
Oiie, tudo bem?
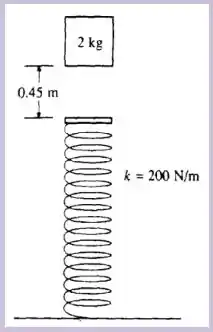
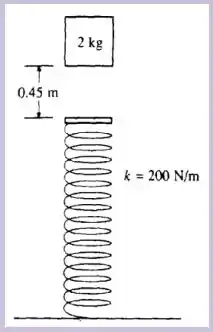
Temos o seguinte esquema que representa bem as informações de nosso enunciado
essa alternativa pede
O período da oscilação.
Para determinarmos essa não precisamos de nenhuma informação das outras alternativas! Apenas determinar a definição de período e frequência natural! Saca só!
Passo 2
Como esse é um MHS temos que a frequência natural é dada por
usando os dados do problema, temos que
e, lembrando que
temos que
Mais uma alternativa já era! Vamos para a última agora!