UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 32d
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A velocidade do bloco na posição de equilíbrio.
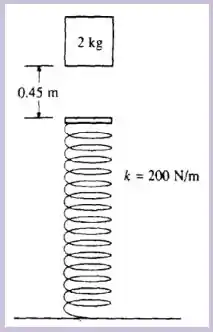
Passo 1
Oiie, tudo bem?
Temos o seguinte esquema que representa bem as informações de nosso enunciado
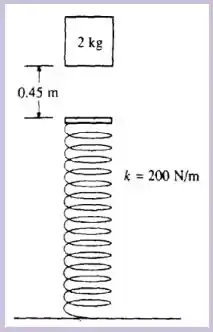
essa alternativa pede
A velocidade do bloco na posição de equilíbrio.
Nas alternativas anteriores encontramos que o bloquinho atinge a mola com velocidade
e, também que a força na posição de equilíbrio é tal que
assim como a compressão da mola até a posição de equilíbrio é
Precisamos encontrar a velocidade na posição de equilíbrio! Para isso vamos ter que usar novamente a conservação da energia mecânica, em que agora teremos a energia mecânica será da forma
em que
, e
Vamos obter a velocidade no ponto do equilíbrio!
Passo 2
Lembrando que na primeira alternativa usamos um referencial que estava na base da mola sem compressão alguma, temos que inicialmente a energia mecânica é somente cinética da forma
Ao chegar na posição de equilíbrio a energia mecânica terá três componentes
essa altura no referencial escolhido é idêntico à
portanto, usando a conservação da energia mecânica, usando , e , temos que
de forma que
de forma que
Mais uma alternativa já era! Vamos para a próxima!