UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 24
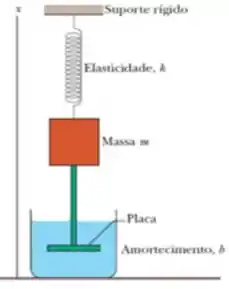
Em um oscilador amortecido como o que está mostrado na figura ao lado, o bloco possui uma massa de e a constante elástica é . A força de amortecimento é dada por , em que . O bloco é puxado para baixo e liberado. Calcule o tempo necessário para que a amplitude das oscilações resultantes diminua para um terço do valor inicial. Quantas oscilações o bloco realiza neste intervalo de tempo?
Passo 1
Oiie, tudo bem?
Temos o seguinte esquema
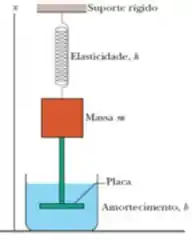
este esquema representa um oscilador harmônico amortecido. Temos que o bloco tem uma massa de e a constante elástica é tal que . Temos uma força de amortecimento proporcional a velocidade da forma
em que . Se fizermos uma distensão inicial de
podemos calcular
O tempo necessário para que a amplitude das oscilações resultantes diminua para um terço do valor inicial e quantas oscilações o bloco realiza neste intervalo de tempo.
Para isso precisamos verificar que tipo de amortecimento temos e usar a solução adequada! Saca só!
Passo 2
Tendo em vista que a questão pede para calcularmos número de oscilações é um bom chute pensar que ela deve ser um amortecimento subcrítico, mas vamos verificar calculando
usando que e , temos que
e, analogamente, temos que
De forma que o delta é dado por
Como temos que , este é um amortecimento subcrítico, e portanto, temos que
Vamos usar isso para calcular o tempo pedido!
Passo 3
Temos que obter o tempo para que a amplitude seja de . A amplitude é obtida sempre que
sendo assim, podemos escrever que
Note que queremos tal que
Sendo assim, buscamos que seja solução para
aplicando o logaritmo em ambos os lados temos que
Aí está! Vamos ver quantas oscilações cabem neste intervalo de tempo!
Passo 4
Para obter o número de oscilações, vamos primeiro calcular a frequência do oscilador amortecido! Não confunda com a frequência natural
temos que o oscilador amortecido tem uma frequência angular calculada por
usando os valores que calculamos ao longo da questão temos que
ou seja, o período é dado pela relação
de forma que
De forma que o número de oscilações até que a amplitude caia em um terço é dada por
oscilações
ou, oscilações completas
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
,