UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 27
Considere um circuito LRC em série onde . O capacitor é carregado com uma carga inicial e então o circuito é colocado para oscilar. Sabendo-se que o período da oscilação não amortecida é de e o coeficiente de amortecimento é , pede-se:
Escreva a equação da oscilação dom todas as constantes numéricas.
Calcule os valores da capacitância e da resistência.
Passo 1
Oiie, tudo certinho contigo?
TEmos um circuito LRC (Indutor Resistor Capacitor) em série da seguinte forma
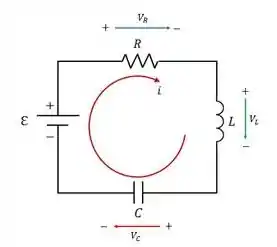
a tensão indicada na figura não nos importa muito agora, mas é ela quem carrega o capacitor inicialmente, ao iniciarmos a oscilação podemos simplesmente retirar a fonte do circuito. Temos que a Indutância é tal que
e a carga inicial é dada por
O enunciado também cita o período da oscilação não amortecida (circuito LC) que tem valor
esse valor será útil para encontrarmos a frequência natural do oscilador. E, por último temos o coeficiente de amortecimento dado por
que está relacionado a introdução do resistor em nosso circuito! O objetivo aqui é construir a equação diferencial que rege a nossa oscilação amortecida, e então usar ela para obter a capacitância e a resistência! Vamos lá!
Passo 2
O que precisamos fazer é aplicar a lei das malhas (segunda lei de Kirchoff) que indica que o potencial dentro de uma malha se conserva, ou seja, temos que
usando que
e que
temos que a equação diferencial toma a forma
em um sistema sem fonte como desejamos, temos que
usando que a corrente elétrica pode ser escrita como
temos que
definindo que
e que
podemos escrever
usando que , em termos de valores numéricos, temos que
Vamos achar agora a capacitância e a resistência!
Passo 3
Temos que
ou seja, a capacitância é dada por
e a resistência é tal que
ou seja, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!