UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 32a
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A velocidade do bloco no instante que ele atinge a mola.
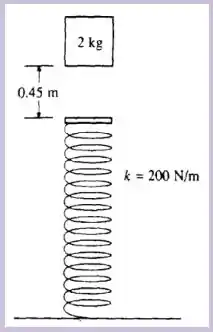
Passo 1
Oiie, tudo bem?
Temos o seguinte esquema que representa bem as informações de nosso enunciado
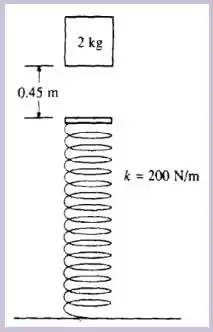
essa alternativa pede
A velocidade do bloco no instante que ele atinge a mola.
Para encontrarmos esta velocidade vamos precisar lembrar das definições de energia potencial gravitacional
e, também da definição de energia cinética
E, não podemos esquecer da conservação da energia mecânica
com essas informações! Temos tudo que precisamos! Vamos lá!
Passo 2
Se considerarmos que a partícula está caindo do repouso, temos que sua energia cinética inicial é
e, escolhendo um referencial no topo da mola (posição de equilíbrio original), temos que a energia potencial será dada por
em que é o comprimento da mola. No limiar de atingir a mola temos que parte da energia potencial gravitacional se transforma em cinética, de forma que
e
Com isso tudo! Agora é só usar a conservação da energia mecânica!
Passo 3
Pela conservação da energia mecânica temos que
portanto, temos que
De forma que a velocidade é dada por
A primeira alternativa foi isso! Vamos para as próximas!