UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 19
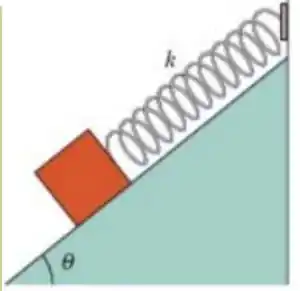
A figura ao lado mostra um bloco com de peso, que pode deslizar sem atrito em um plano inclinado de ângulo e está ligado ao alto do plano inclinado por uma mola, de massa desprezível, de de comprimento quando relaxada, cuja constante elástica é . A que distância do alto do plano inclinado fica o ponto de equilíbrio do bloco? Se o bloco é puxado ligeiramente para baixo ao longo do plano inclinado e depois liberado, qual é o período das oscilações resultantes?
Passo 1
Eaew, tudo bem?
O enunciado nos dá o seguinte esquema
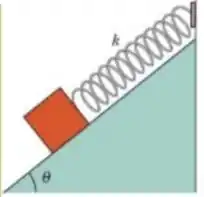
O bloco pesa
e o plano inclinado é feito de um material que permite que o bloquinho deslize livremente. Temos que a inclinação é de e que a mola que liga o bloco ao topo do plano tem um comprimento de
a mola tem massa desprezível! Nós temos que analisar essa situação e encontrar a posição de equilíbrio
do oscilador, assim como a frequência de oscilação deste sistema! Este é um sistema bastante similar a um oscilador harmônico vertical, portanto, a força constante existente devido a componente do peso ao longo do plano irá causar apenas uma variação na posição de equilíbrio, a qual iremos determinar no próximo passo! A frequência será obtida como usualmente em problemas de MHS! Saca só!
Passo 2
Temos que a componente do peso ao longo do plano é tal que
De forma que a equação diferencial do oscilador harmônico se torna
vamos reescrever a equação acima da seguinte maneira
Se fizermos a seguinte mudança de variáveis
temos que
Que é a equação de um oscilador harmônico usual que tem como posição de equilíbrio
usando a constante da mola dada, temos que
Essa é a primeira alternativa! Vamos achar agora o período!
Passo 3
Como citei no primeiro passo, a translação causada pela força constante não altera a forma usual usada para calcular o período, usando que
podemos multiplicar e dividir numerador por e obter que
ou simplesmente
usando então que
Obtemos a frequência como
E, finalmente, o período como
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
,