UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 32e
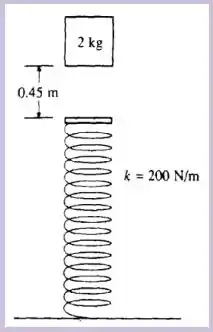
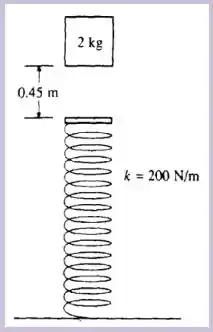
Um bloco de cai verticalmente sobre a extremidade de uma mola que se localiza à abaixo. A mola tem massa muito pequena (desprezível) e se encontra descomprimida e sua constante elástica é de . Ao atingir a mola o bloco fica preso a ela. Com essas informações e considerando , calcule:
A amplitude da oscilação resultante
Passo 1
Oiie, tudo bem?
Temos o seguinte esquema que representa bem as informações de nosso enunciado
essa alternativa pede
A amplitude da oscilação resultante
Nas alternativas anteriores encontramos que o bloquinho atinge a mola com velocidade
e, também que a força na posição de equilíbrio é tal que
assim como a compressão da mola até a posição de equilíbrio é
e a velocidade na posição de equilíbrio como
novamente teremos que utilizar a conservação da energia mecânica, neste caso definida como
em que
, e
Vamos ter que encontrar o momento em que toda a energia cinética se transforma em energia potencial elástica! Saca só!
Passo 2
Temos que o bloco colide com a mola com uma velocidade
portanto, tem uma energia cinética dada por
Essa energia tem que ser toda transformada em potencial gravitacional e potencial elástica para que encontremos a compressão máxima da mola, ou seja, temos que
nesta escolha de referencial, temos que
portanto, temos que resolver o polinômio
ou usando alguns valores conhecidos
usando Bhaskara temos que
Que será a amplitude da oscilação! Vamos para a próxima alternativa agora!