Avalie a integral:
Passo 1
Procurar por descontinuidades
Essa integral parece tranquila né? Só integrar e aplicar os limites e ir pro abraço! Infelizmente, não é só isso. Dá uma olhada:
Portanto nossos limites de integração estão exatamente “abraçando” um ponto de descontinuidade. Quando isso acontece, é possível que a nossa integral não venha a convergir. Puts, nesse caso então, vamos ter que trabalhar com limites e integrais, não é? É sim! Vamos reescrever então:
Passo 2
Resolver a integral
Vamos então sumir com a integral pra podermos trabalhar só com limites beleza? Sendo assim, vamos calcular:
Fazendo a substituição simples:
Vamos ficar com:
Voltando a variável original
Passo 3
Aplicando os limites de integração
Beleeeza, resolvemos a integral. Vamos então aplicar os limites de integração pra depois finalmente poder resolver os limites e . Partiu:
Passo 4
Aplicando os limites e
Resumindo tudo que pescamos até agora, temos:
Show de bola, só juntar tudo agora. Nossa integral vai ficar:
E aqui morre o problema porque
São limites que não convergem por causa da descontinuidade! Sendo assim:
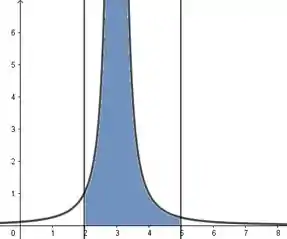
Graficamente, é como se fossemos calcular a área dessa região que tem altura infinita. Ia ser complicado, não?