Verifique se as integrais abaixo são convergentes ou divergentes.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão foi dada uma integral e temos que verificar se essa integral converge ou diverge.
Mas como assim? Converge ou diverge?? 🤔
Perceba que a função de integração possui uma descontinuidade em , já que nesse ponto o denominador da função vai a .
Nesses casos, vamos aplicar a ideia de integrais improprias calculando a integral em duas integrais separadas pelo ponto de descontinuidade no intervalo de integração.
Se a soma das integrais resultar em uma constante, significa que a integral converge, caso o contrário, não diverge.
Entendeu? Bora começar os cálculos! 😉
Passo 2
Inicialmente, nosso intervalo dos limites de integração vai de . Mas como em , a função é descontinua, temos que separar esse intervalo em dois e .
Perceba que não pode ser incluso nos limites de integração, então vamos obter os valores que a função assume quando tende a esse valor, ou seja
Entendeu o que fizemos?
Vamos começar calculando a integral sem os limites de integração
Vamos usar o método de substituição fazendo e consequentemente
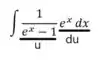
Fazendo as substituições
Essa integral é bastante conhecida, não é? Ela resulta em
Substituindo por de volta...
Tranquilo até aqui? 😎
Passo 3
Resolvendo a primeira integral, aplicando os limites de integração, temos
Como o limite da soma é igual à soma dos limites...
O primeiro limite é uma constante, logo se o limite de uma constante é igual a constante...
Quando tende a pela direita, tende a com valores positivos dentro do . Lembra do gráfico de ?
Para valores muito pequenos de , a imagem tente a , veja só
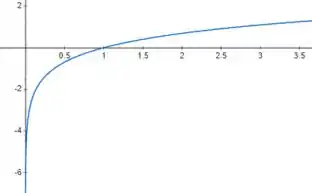
Então podemos afirmar que
Então a integral dessa parcela do intervalo resulta em
Perceba que já temos uma divergência nessa parte da integral pois temos como resultado .
Quando isso acontece, podemos afirmar que a integral diverge sem nem precisar calcular a outra parte.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍