Lista 4.14 – Integrais impróprias com integrandos descontínuos – UFSC – Cálculo 1 – Questão 1d
Quais das integrais abaixo são impróprias? Por quê?
(d)
Passo 1
Falaee, beleza?? Se liga.. vamos dar uma olhadinha no gráfico da função .
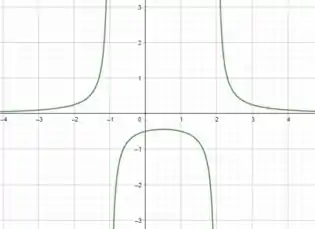
Passo 2
Perceba novamente que se , o denominador será igual a , fazendo com que a função tenda ao infinito.
Dessa forma, havendo uma descontinuidade nos limites de integração, a integral é imprópria!!
Entendeu direitinho? Responde aee ;)
Resposta
A integral é imprópria
Exercícios de Livros Relacionados
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 1 1 1 - x 2d x
Investigar as integrais impróprias.
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 1 3 x 5d x
Explique por que cada uma das seguintes integrais é imprópria. ∫ 1 ∞ x 4 e - x 4 d x ∫ 1 π 2 sec x d x ∫ 0 2 x x 2 - 5 x + 6 d x ∫ - ∞ 0 1 x 2 + 5 d x
Calculeb)int_(- 1)^3 f (x) d x ondef (x) = {[[1 s e - 1 = x0],[x^2 s e 0x2],[0 s e 2 = x = 3]])