Lista 4.13 – Testes de convergência de integrais impróprias– UFSC – Cálculo 1 – Questão 3d
Sefa uma função contínua e limitada. A Transformada de Laplace de é a função definida por
- Encontre a transformada de Laplace de .
Passo 1
Falaee, beleza?? Se liga.. a gente sabe que a Transformada de Laplace é dada por:
Agora, é só fazer . Vamos lá!!
Passo 2
Substituindo, temos:
Agora, vamos integrar por partes. Lembrando que a integral por partes é dada por:
Em que:
Passo 3
Assim, temos:
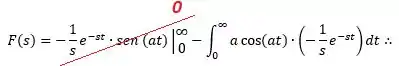
Fazendo novamente por integral por partes, temos:
Passo 4
Substituindo, temos:
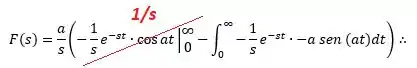
Porém, sabe-se que .
Logo, temos a seguinte equação:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 1 1 1 - x 2d x
Investigar as integrais impróprias.
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 1 3 x 5d x
Explique por que cada uma das seguintes integrais é imprópria. ∫ 1 ∞ x 4 e - x 4 d x ∫ 1 π 2 sec x d x ∫ 0 2 x x 2 - 5 x + 6 d x ∫ - ∞ 0 1 x 2 + 5 d x
Calculeb)int_(- 1)^3 f (x) d x ondef (x) = {[[1 s e - 1 = x0],[x^2 s e 0x2],[0 s e 2 = x = 3]])