UFF, Sem Campus, Física 1, Listas de Física 1 - Profº Marcos Sergio - Lista 1, Questão 10
Um arqueiro parado em um declive de atira uma flecha acima do horizontal, conforme mostrado na figura ao lado. A que distância da encosta (alcance) a flecha atinge o solo se for atirada com uma velocidade de de um ponto que dista do solo?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos mostra um arqueiro em um declive onde atira uma flecha de tal forma que podemos representar a seguinte figura (já colocando os dados da questão):
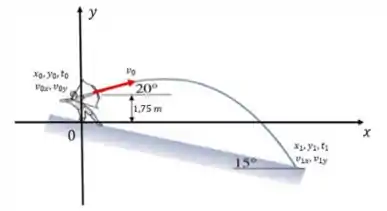
Pelo lançamento oblíquo e pelo enunciado, temos que:
Onde o objetivo é encontrar a distância sobre a rampa que a flecha atingirá!
Por fim, basta usarmos o Teorema de Pitágoras!!
E aí? Bora lá??!!
😉
Passo 2
Assim, fazendo primeiramente para a horizontal, observando a figura, temos:
Passo 3
Agora, para a vertical, utilizando a equação da posição em função do tempo, temos:
Passo 4
Por fim, sabemos que a flecha atinge o solo formando um ângulo de com a horizontal, no sentido horário, ou seja:
Obs: o ângulo fica negativo porque estamos adotando o sentido horário.
Assim, substituindo as equações dos Passos anteriores, temos:
Resolvendo essa equação do segundo grau, encontramos:
Logo, como só trabalhamos com tempo positivo, então .
Passo 5
Como descobrimos o valor de , basta substituirmos nas equações dos Passos 2 e 3:
E
Passo 6
Por fim, fazendo o Teorema de Pitágoras, descobrimos a distância com que a flecha atinge o solo:
Entendeu direitinho? Responde aee ;)
