Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lançamento Oblíquo

Ver Teoria
Exercício 113123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFF, Sem Campus, Física 1, Listas de Física 1 - Profº Marcos Sergio - Lista 1, Questão 8b

Um avião mergulhando com velocidade constante num ângulo de 53,0 ° com a vertical libera um projétil a uma altitude de 730   m . O projétil bate no chão 5,0 s após ter sido liberado.

b) Que distância o projétil percorre horizontalmente durante o seu vôo?

Passo 1

Eaee!!! Belezinha? Bom... a questão nos pergunta qual distância o projétil percorre horizontalmente durante o seu vôo.

Para isso, é sempre bom lembrar que no momento da liberação do projétil, o avião estava mergulhando com velocidade constante num ângulo de 53,0 ° com a vertical, ou seja:

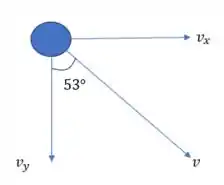
Dessa forma, podemos dizer que suas componentes vertical e horizontal são, respectivamente:

v y = v cos ⁡ 53 °

v x = v sin ⁡ 53 °

Da questão anterior, descobrimos que v = 202   m / s .

Nesse sentido, podemos descobrir a velocidade do avião na horizontal e, com isso, encontraremos a distância percorrida!!

E aí? Bora lá??!!

😉

Passo 2

Assim, sabemos que a velocidade do avião na horizontal é:

v x = 202 * sin ⁡ 53 ° ∴

v x = 161,3   m / s

Logo, a distância percorrida é dada por:

v x = Δ S Δ t

Onde Δ S é a distância percorrida na horizontal e Δ t é a variação do tempo. Logo:

Δ S = 161,3 * 5 ∴

Δ S = 806,5   m

Entendeu direitinho? Responde aee ;)

Resposta

Δ S = 806,5   m

Exercícios de Livros Relacionados

Suponha que o ângulo inicial α 0 da Figura 3.26 seja 42,0 ° e que d seja igual a 3,0 m. Onde o dardo e o macaco se encontrarão, se a velocidade inicial do dardo for a) 12,0 m/s? b) 8,0 m/s?c) O que oc
Galileu mostrou que, se os efeitos da resistência do ar são ignorados, os alcances de projéteis (no mesmo nível) cujos ângulos de projeção diferem de 45°, para mais e para menos, do mesmo valor, são i
Em 1939 ou 1940 , Emanuel Zacchini levou seu número de bala humana a novas alturas: disparado por um canhão, passou por cima de três rodas-gigante antes de cair em uma rede (Fig.4-39). (a) Tratando Za
Os esquiadores experientes costumam dar um pequeno salto antes de chegarem a uma encosta descendente. Considere um salto no qual a velocidade inicial é v 0 =10m / s , o ângulo é θ 0 =9,0 ° , a pista a
Cortina da morte. Um grande asteroide metálico colide com a Terra e abre uma cratera no material rochoso abaixo do solo, lançando pedras para o alto. A tabela a seguir mostra cinco pares de velocidade