Um balão de São João, partindo do repouso, é empurrado pelo vento e desloca-se horizontalmente a uma altura do solo. Devido ao vento, a aceleração do balão é Após do início deste movimento, o balão incendeia-se instantaneamente. A tocha, sobre a qual o efeito do vento é desprezível, cai e acaba atingindo uma casa. A altura da casa é e se encontra a uma distância horizontal, a contar do ponto em que o balão incendiou-se, como mostrado na figura. Pergunta-se: qual é o vetor velocidade da tocha quando ela atinge o telhado? Dê suas respostas na base de vetores (, )
Despreze a resistência do ar.
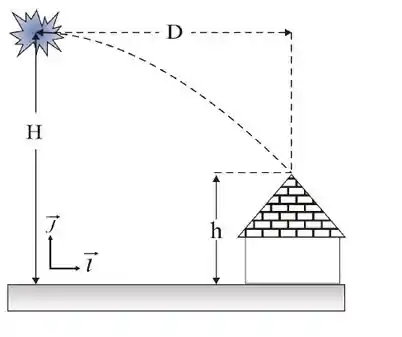
Passo 1
Vamos por partes...
No início, temos um movimento acelerado tanto na direção x quanto na y. As acelerações valem:
Notem que em x temos uma aceleração que varia com o tempo, então não podemos usar as equações do MUV. Para a direção y, temos a aceleração constante, então ok usar as equações do MUV.\
Como a aceleração de x varia com o tempo, vamos usar:
Até os primeiros 60 s, a tocha está junto com o balão, após isso eles se separam, mas a tocha não sente mais a aceleração do vento, ou seja, após os 60 s a velocidade em x vai permanecer constante, teremos um movimento uniforme, então vamos descobrir qual vai ser essa velocidade
Show! Então essa velocidade vai permanecer constante enquanto a tocha cai na casa. Então já sabemos a componente x da velocidade nesse instante.
Vamos ver agora na direção y, onde temos um muv, já que a aceleração é constante.
Vimos que ele parte do repouso e que
Então
E qual é o tempo? É o tempo que ele leva pra cair na casa, ou seja:
ou seja o tempo de queda é:
Substituindo:
Substituindo os valores, temos que a componente y da velocidade quando a tocha chega na casa é:
Então o vetor velocidade pode ser escrito como: