UFABC – Fundamentos de Mecânica – Lista 2 – Questão 10
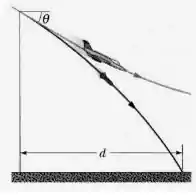
Um certo avião tem uma velocidade de 290,0 km/h e está mergulhando em um ângulo abaixo da horizontal quando o piloto libera um míssil despistador (figura abaixo). A distância horizontal entre o ponto de lançamento e o ponto onde a isca bate no solo é.
(a) Quanto tempo a isca fica no ar?
(b) De que altura ela foi liberada?
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou fazer passo a passo com você!
Temos um avião que solta uma isca (despistador) no ar. A velocidade inicial dessa isca será a mesma do avião, já que os dois se movimentam juntos até o instante em que ela é solta. Depois essa isca passa a cair em queda livre na direção vertical. Na horizontal segue tendo a mesma velocidade inicial, já que não temos aceleração nessa direção.
Então a ideia para resolver questões de lançamento oblíquo é:
- Achar a velocidade inicial nas direções x e y a partir do ângulo dado,
- Com o deslocamento horizontal podemos encontrar o tempo de queda (o tempo que a isca leva para cair é o mesmo que ela leva se deslocando para o lado)
- E com o tempo de queda (e a velocidade inicial em y) podemos usar a equação horária do MRUV para achar a altura inicial.
Mas calma, vou fazer junto com você!
Vamos lá?
Passo 2
O movimento como um todo pode ser dividido em movimento uniforme em relação ao eixo e movimento uniformemente variado em relação ao eixo , beleza?!
A primeira coisa que devemos fazer é calcular a velocidade inicial em relação aos dois eixos:
Eixo x:
Se você reparar, o avião está mergulhando abaixo da horizontal, então a direção será , beleza?!
Eixo y:
Mesmo raciocínio anterior,
Agora vamos converter para !!
Sabemos que:
Logo,
Show de bola?!
Passo 3
Letra (a):
Beleza, agora que já sabemos a distância percorrida pelo projétil na horizontal e a velocidade inicial dele nessa direção, podemos calcular o tempo que ele permaneceu no ar através da relação:
Tranquilo? Vamos para o segundo item?
Passo 4
Letra (b):
Agora que sabemos o tempo que o projétil levou para chegar ao solo e já sabemos sua velocidade inicial em relação ao eixo y, podemos achar a altura de que foi lançado através da relação:
Assim,
Substituindo os valores:
E é isso!
Espero ter ajudado!