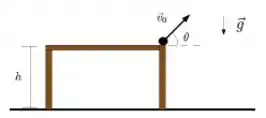
Um corpo de massa é lançado no instante com velocidade de módulo do topo de uma mesa de altura com relação ao solo, conforme a figura abaixo. A altura máxima que o corpo atinge com relação ao solo é e o tempo que leva para o corpo atingir essa altura é . Além disso, o tempo total até o corpo atingir o solo é . Despreze efeitos oriundos da resistência do ar. Assumindo que , marque a resposta correta abaixo:
Dado: (capa da prova)
(a) ,,
(b) , ,
(c) , ,
(d) , ,
(e) , , .
Passo 1
A bola é lançada da mesa com sua velocidade fazendo uma inclinação de com a horizontal. Então, temos um caso de Lançamento Oblíquo.
Costumamos trabalhar, nesses casos, separadamente com a componente horizontal e a componente vertical do movimento da bola.
Mas por que?
Isso porque a única aceleração atuando sobre a bolinha é a aceleração da gravidade (constante) e ela está apenas na vertical. Com isso, o movimento na vertical terá uma aceleração constante, enquanto o movimento na horizontal não terá nenhuma aceleração, logo seus movimentos em cada eixo serão:
Nosso objetivo envolve três coisas:
Passo 2
Vamos começar achando o tempo que a bola leva para atingir a altura máxima .
Para isso, vamos analisar o movimento na vertical primeiro.
A gente acabou de ver que na vertical, como a aceleração é constante, a bola realiza um , então, podemos usar a equação da velocidade para esse movimento:
Mas por que usar a equação da velocidade em vez da posição?
Simples, é porque não conhecemos exatamente a posição máxima ainda e além disso, sabemos que quando a partícula atinge a altura máxima é porque ela parou momentaneamente, ou seja, sua velocidade nesse instante é nula:
Passo 3
A aceleração nós já sabemos, ela vale e considerando um referencial positivo para cima, ela será negativa pois aponta para baixo:
Mas quem é a velocidade inicial na vertical ?
Vamos decompor o vetor velocidade inicial em suas componentes:
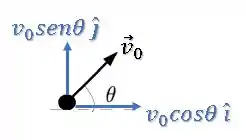
Então:
Substituindo esse valor de velocidade inicial na equação, temos:
Pronto!
Passo 4
Agora, basta considerar o instante e que a partícula atinge a altura máxima, tendo velocidade zero, para achar quanto tempo ela leva até isso:
Substituindo os valores de , e , temos:
Jogando essa raiz quadrada para o denominador (de olho nas respostas), temos:
Por eliminação, já ficamos entre a letra (a) e (e), mas vamos achar todos os parâmetros pedidos para encontrar a resposta.
Passo 5
Agora, vamos encontrar a altura máxima medida a partir do chão.
Ainda no movimento vertical, a equação da posição para um vai ser:
A altura inicial é , enquanto e nós já sabemos do outro item:
Passo 6
Como já achamos o tempo que leva até ser atingida a altura máxima, basta substituir isso na expressão:
Se quiséssemos a expressão algebrica primeiro, ficamos com:
Mas como já calculamos o , é mais fácil substituir direto o valor pronto:
Substituindo os outros dados (, , ) ficamos com:
Fazendo o MMC, temos:
Agora já confirmamos que a resposta é a letra (e), mas vamos achar o também, por que não né? hahah
Passo 7
Para encontrar o tempo que a bola leva até o chão, basta a gente considerar a psoição final como zero (altura do chão):
Repara que agora caímos em uma equação do segundo grau, então podemos usar o Bháskara.
Mas antes, vamos substituir os valores numéricos que conhecemos para não ficar tão poluído:
Colocando na ordem que estamos mais acostumados:
Deu para enxergar melhor agora?
Passo 8
Vamos lá, então:
Sendo , e os coeficientes que multiplicam .
Que é igual a:
Essa é uma malandragem que a gente faz para a resposta dentro da raiz quadrada bater com a da alternativa.
Substituindo agora na solução de Bháskara:
Das duas opções , apenas essa resulta em um tempo positivo:
Finalmente temos que:
Resposta
Letra (e)