UFABC – Fundamentos de Mecânica – Lista 2 – Questão 12
Durante erupções vulcânicas, grandes pedaços de rocha podem ser ejetados para fora do vulcão; estes
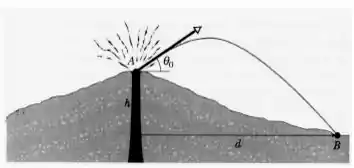
projeteis são chamados de bombas vulcânicas. A figura abaixo mostra a seção transversal do Monte Fuji, no Japão.
(a) Com que velocidade inicial uma bomba teria que ser ejetada, em um ângulo em relação à horizontal, a partir da abertura A, de modo a cair na base do vulcão em B, a uma distância vertical h = 3; 30 km e a uma distância horizontal d = 9; 40 km?
(b) Ignorando os efeitos do ar sobre o movimento da bomba, qual seria o tempo de voo?
(c) O efeito do ar aumentaria ou diminuiria sua resposta ao item (a)?
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Essa é uma questão de lançamento de projétil, na qual precisamos lembrar das equações que dão as coordenadas e de um corpo que é lançado com uma velocidade e um ângulo com a horizontal:
A ideia para resolver esse problema é utilizar essas duas equações para determinar o que queremos! Lembrando que o tempo de voo (que é o tempo que o projétil leva para chegar até o chão, a partir do lançamento) é o mesmo que ele leva para se deslocar horizontalmente.
E para facilitar nossa vida, podemos admitir que .
Mas calma, vou fazer passo a passo com você!
Passo 2
Letra (a):
Então pessoal, utilizando as equações do movimento oblíquo, podemos isolar na equação de e substituir na de , e assim obtemos a velocidade inicial!
De :
E agora substituir na equação para e considerando :
E agora isolar :
Certo? Utilizando , e , obtemos o valor da velocidade inicial:
Vamos para a letra (b)?
Passo 3
Letra (b): tempo de voo
Bom pessoal, para calcular o tempo que a bomba vulcânica permanece no ar basta utilizarmos a fórmula para do passo 1:
Beleza?
Agora o último item!
Passo 4
Letra (c):
Então galera, é intuitivo imaginar que o ar ofereça uma certa resistência ao movimento, assim considerando essa resistência seria necessária uma maior velocidade de lançamento para atingir a mesma distância.
Sendo assim, levando em conta o ar, a velocidade inicial aumentaria para compensar o efeito resistivo do ar.
E é isso!
Espero ter ajudado!