[Enunciado comum às Questões 1 e 2]
Uma bola é lançada com velocidade acima da horizontal e leva para atingir a parede.
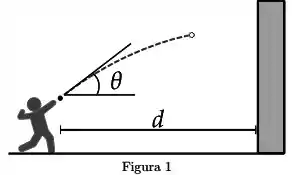
[Questão 1]
Considere as seguintes assertivas:
. A distância da parede ao ponto de lançamento é de
. A trajetória da bola é uma parábola.
. A bola atinge a parede após atingir o ponto mais alto da sua trajetória
É correto apenas o que se afirma em: ́
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Temos um Lançamento Oblíquo, e em um movimento assim, costumamos trabalhar separadamente com o movimento na horizontal e na vertical.
Para facilitar nossa vida, já temos a velocidade em cada componente já separada:
Fazemos isso porque a única força atuando sobre a pedra ao longo da trajetória está na vertical para baixo, a famosa força Peso.
Assim, o movimento na horizontal será um Movimento Uniforme, já que não tem nenhuma força atuando nessa direção.
Já o movimento na vertical será um Movimento Uniformemente Variado, pois temos uma aceleração constante para baixo (gravidade).
Vamos dar uma olhada nas alternativas e checar quais são verdadeiras.
Passo 2
. A distância da parede ao ponto de lançamento é de
Para descobrir essa distância da parede, vamos trabalhar com o movimento horizontal.
Olhando para o vetor velocidade:
Qual é a velocidade na componente ?
É a componente do vetor unitário , então:
Essa velocidade vai se manter ao longo de toda a trajetória, então podemos usar aquela equação da posição para um Movimento Uniforme:
Como o a pedra leva para atingir a parede, temos:
A afirmativa é verdadeira.
Passo 3
. A trajetória da bola é uma parábola.
Isso é verdadeiro!
Na horizontal, a posição varia uniformemente (linear) com relação ao tempo, enquanto na vertical a posição varia com o quadrado do tempo. Essa combinação gera uma parábola.
Em todo lançamento (exceto o vertical), a trajetória será uma parábola!
A afirmativa é verdadeira.
Passo 4
. A bola atinge a parede após atingir o ponto mais alto da sua trajetória
Qual é o ponto mais alto de sua trajetória?
Na verdade não precisamos saber a exata posição para depois comparar com a posição que ela atinge a parede.
Podemos usar o fato de que, na vertical, a partícula para (velocidade zero) no ponto mais alto de sua trajetória.
Então, vamos checar se sua velocidade chega a zero antes ou depois de (instante em que bate na parede).
Em um Movimento Uniformemente Variado, podemos usar essa equação para a velocidade:
Quem é a velocidade vertical inicial?
Vai ser a componente do vetor unitário :
Substituindo esse valor na equação e, além disso, colocando a aceleração como a aceleração da gravidade () com o sinal negativo, já que aponta para baixo, temos:
No instante de altura máxima, a velocidade é zero, então:
Isso significa que a pedra levaria aproximadamente para atingir o ponto máximo de sua trajetória, então, ela bate na parede antes disso acontecer.
A afirmativa é falsa.
As afirmativas corretas são a e , ficamos com a letra (d).
Resposta
Letra (d)