Um professor de física faz proezas loucas em suas horas vagas. Sua última façanha foi saltar sobre um
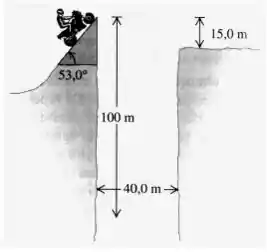
rio com sua motocicleta. A rampa de decolagem era inclinada de 53,0o, a largura do rio era de 40,0 m, e a outra margem estava a 15,0 m abaixo do nível da rampa. O rio estava a 100 m abaixo do nível da rampa. Despreze a resistência do ar.
(a) Qual deveria ser sua velocidade para que ele pudesse alcançar a outra margem sem cair no rio?
(b) Caso sua velocidade fosse igual a metade do valor encontrado em (a), onde ele cairia?
Passo 1
Olá, tudo bem? Essa questão parece complicada, mas vou ajudar você =) Vamos lá?
Primeiro vamos escolher um sistema de coordenadas. Vou escolher como origem dos espaços a posição inicial da moto. Também vou considerar para cima o sentido positivo do eixo e para a direita, para .

O problema pede que se ache a velocidade inicial para que a moto chegue na posição e . Mas não sabemos nem a velocidade inicial e nem o tempo de voo. Então a ideia é montar duas equações com essas duas variáveis para que possamos eliminar uma delas e determinar .
Mas quais são essas equações? Ora, são as equações do movimento! Sabemos que na horizontal o movimento é uniforme e na vertical é variado.

Passo 2
Letra (a): As equações de movimento são:
E os dados que temos são:
Então as equações ficam assim:

Da primeira equação, quando temos podemos ter o tempo em função da velocidade:
E substituindo na segunda equação com , conseguimos eliminar e ficar só com , saca só:
Agora vamos simplificar um pouco:
E resolver para :
Beleza? Vamos calcular o próximo item?

Passo 3
Letra (b):
Agora o problema pergunta onde a moto cairia se ela tivesse metade da velocidade que encontramos na letra , ou seja, se .

Mas vamos pensar uma coisa juntos: se a velocidade que encontramos antes é a velocidade mínima necessária para ele atravessar o rio sem cair nele, então com uma velocidade menor ele com certeza irá atingir o rio, certo?

Então o problema se resume a descobrir o alcance horizontal quando a posição final dele vai ser .
As equações de movimento são as mesmas:
Mas agora com os seguintes dados:
Como não sabemos o tempo de voo, primeiro vamos usar a segunda equação para determinar o instante que a moto chega ao rio, para depois substituir na primeira e assim determinar . Vamos lá?

Da segunda equação:
Temos uma equação de segundo grau e as raízes são calculadas por bhaskara:
E o que vale é a raiz positiva, então o instante que a moto chega no rio é .
Agora substituindo na primeira equação:
E essa seria a posição que ele cairia!

E é isso!
Espero ter ajudado!