Você está a de uma parede da casa vista na figura ao lado. Você quer jogar uma bola para seu amigo que está a da parede oposta. O arremesso e a recepção ocorrem a acima do solo.
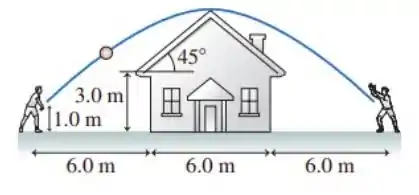
- Que velocidade mínima permitirá que a bola ultrapasse o teto?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular a velocidade mínima permitirá que a bola ultrapasse o teto de uma casa esquematizada da seguinte forma:
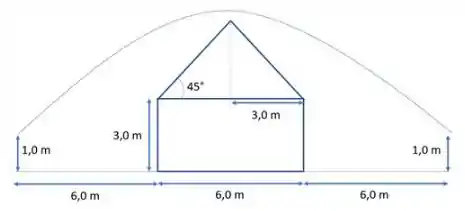
Para isso, precisamos descobrir a altura máxima para que a bola consiga ultrapassar a casa.
E aí? Bora lá??!!
😉
Passo 2
Bom... geometricamente o telhado é um triângulo isósceles, ou seja, podemos destacar ele pela seguinte representação onde vemos a sua altura (de ):
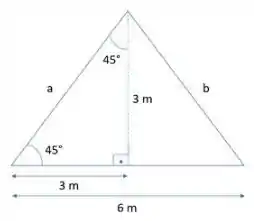
Assim, sabemos que a altura da casa é de .
No entanto, como estamos considerando que a bola é lançada a de altura, então a altura máxima do movimento em relação a é de:
.
Passo 3
Dessa forma, podemos encontrar a velocidade inicial mínima para que a bola ultrapasse o teto e chegue ao outro lado.
Mas primeiro, utilizando a equação de Torricelli, podemos encontrar a velocidade mínima na vertical (lembrando que a velocidade final na altura máxima é zero):
Passo 4
Agora, para descobrir a velocidade na horizontal (onde trata-se de um movimento uniforme), temos que saber da equação da posição em função do tempo :
E, para descobrir o tempo , podemos utilizar a outra equação da posição em função do tempo para o movimento uniformemente variado na vertical (afinal o tempo é igual para os dois movimentos):
Resolvendo a equação do segundo grau, temos que:
Logo, consideramos .
Assim, aplicando em , temos:
Passo 5
Por fim, podemos descobrir o módulo da velocidade mínima que permitirá que a bola ultrapasse o teto:
Entendeu direitinho? Responde aee ;)
