UFSCAR – Cálculo 2 – Banco de Questões – Questão 2
Considere a função e a curva . O valor de é:
Escolha uma opção:
- -1
- 7
- 5
- 0
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas estou aqui para te ajudar! Vamos resolver juntos?
é a composição da função (que é função de x e y) pela função (que é apenas em t). E o enunciado quer a derivada dessa composição, aplicada em .
Como relembrar é viver, a composição de uma função funciona mais ou menos assim:
“A gente pega a variável da função que tá ‘mais por fora’ e substitui pela função que está por dentro.”
No nosso exercício, a função que está mais por fora é a e a de dentro é a :
E agora as variáveis vão ser substituídas pelas componentes da função . A primeira componente entra no lugar do , a segunda componente entra no lugar do e a terceira, entra no lugar de .
A função é:
Aí a gente vai fazer a substituição das componentes de cada cor:
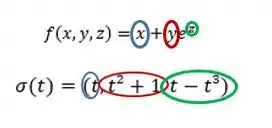
Aí a função em fica assim:
Passo 2
Agora que temos a função em , vamos derivar:
No primeiro termo, é uma simples derivação de polinômio, mas vamos fazer o segundo e o terceiro termos com calma aqui. No terceiro termo, aplicamos a regra da cadeia, pois temos uma exponencial com uma função de no expoente.
E no segundo termo, temos essa mesma exponencial multiplicada por . Então usamos a regra do produto e a regra da cadeia:
Então a derivada da função fica assim:
Tranquilo?
Passo 3
E agora por fim vamos aplicar em :
Aí a alternativa que tem esse resultado é a letra (a).
Belezinha?
Espero ter te ajudado!
Até a próxima =)