Um bloco de massa e com velocidade inicial na parte horizontal do trajeto, sobe uma superfície circular sem atrito de raio .
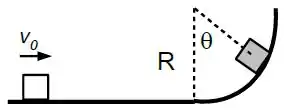
Dados:
a) Determine o módulo da velocidade do bloco na posição ilustrada na figura se .
b) Determine o valor da força normal que age no bloco nesta mesma posição.
Passo 1
Como não há atrito, a energia mecânica do sistema se conserva:
Isso também acontece pois a força normal atua sempre perpendicular ao plano e a caixa desliza na direção do plano, ou seja, essa força não realiza trabalho.
Passo 2
Na letra (a), queremos a velocidade do bloco na posição subindo na rampa com uma angulação de .
Então, vamos conservar a energia em um momento antes do bloco atingir a rampa e no instante final, onde ele está na posição da figura.
Inicialmente, o bloco apresenta apenas energia cinética associada a sua velocidade :
Já na posição da figura, o bloco apresenta tanto uma energia cinética quanto uma energia potencial gravitacional:
Mas qual a altura que a caixa subiu a partir da altura do chão?
Passo 3
Para encontrar essa altura, vamos olhar para o triângulo com o ângulo .
A altura do bloco é essa:
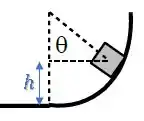
Nós conhecemos o raio :
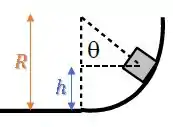
E podemos achar aquele trecho que falta, usando o cosseno de :
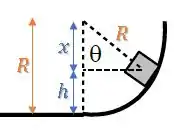
Assim, temos que é:
Passo 4
Voltando à conservação de energia, temos:
Substituindo o valor de :
Costando a mass e fazendo o MMC, temos:
Substituindo os valores, temos:
O ângulo é:
Então:
Ou seja, o bloco atinge aquele ponto com velocidade zero (ponto de altura máxima).
Passo 5
Na letra (b), queremos a força normal que age nessa posição.
Sabemos que a força normal é sempre perpendicular à superfície:
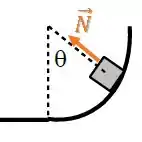
Mas como podemos conseguir uma relação para essa força?
Como a trajetória da rampa é circular, a força resultante na direção radial (mesma direção da normal) deve atuar como força centrípeta:
E nós conhecemos uma expressão para força centrípeta. É essa aqui:
Mas lembra que na letra (a), vimos que o bloco está parado nessa posição?
Ahh, então, nesse instante a força centrípeta é zero:
Assim, vamos usar a relação de que a força resultante nessa direção é nula.
OBS: A força resultante apenas na direção radial é zero. Isso não significa que a força resultante total sobre o bloco é nula, pois ainda existe uma aceleração na direção tangencial (mesma direção da rampa) causada pela componente da força peso .
Passo 6
Agora vamos achar a força resultante na direção radial.
Quais são as forças atuando sobre o bloco?
Além da força normal , temos também a força peso :
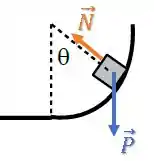
Passo 7
Agora, vamos decompor a força peso em suas componentes na direção radial e tangencial.
Aquele ângulo aparece no ponto de aplicação de :
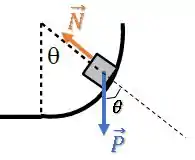
Então, temos:
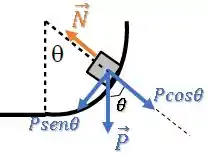
A força resultante na direção radial (que aponta para o centro da trajetória circular) é:
Substituindo os valores, temos:
Resposta
(a)
(b)