UFRJ, Física 1, P2 2019.1, Problema 2 – Concservação De Energia e Leis de Newton
Um bloco de massa m é empurrado contra uma mola de constante elástica k, e comprimento natural , por uma distância x, sendo mantido preso por um pequeno trinco. Quando o trinco é liberado, a mola expande-se empurrando o bloco. Ao passar pela posição de equilíbrio da mola, a mola perde contato com o bloco. O bloco segue adiante deslizando ao longo de uma superfície lisa e sem atrito, até passar a deslizar pelo interior de um aro circular de raio R. Sabendo que no ponto mais alto da trajetória dentro do aro o módulo da força do aro feita sobre o bloco (força normal) é igual a duas vezes o módulo da força peso do bloco. Suas respostas devem ser dadas em termos de m, , k, R e g:
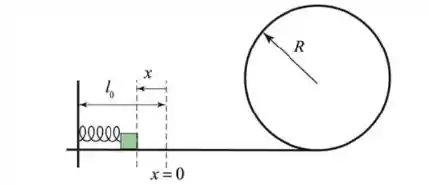
a) Indique quais as forças que atuam sobre o bloco quando ele passa pelo ponto mais alto do aro.
b) Determine a velocidade do bloco no ponto mais alto da trajetória dentro do aro.
c) Determine a compressão inicial, x, da mola. Justifique claramente as Leis de Conservação utilizadas.
Passo 1
- No ponto mais alto temos apenas a força Peso e a Normal! Tranquilo?
- Na letra A a gente sabe que a resultante das forças será P+N, certo? Mas se ele ta num circulo qual será a força resultante nesse corpo?
- Pra gente descobrir a deformação dessa mola a gente pode usar conservação de energia mecânica, lembra? Considerando o chão tendo altura h=0, no começo a gente tem apenas a energia potencial elastica que empurra o bloco, e no ponto mais alto temos a energia potencial gravitacional e a energia cinética, então temos que:
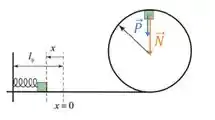
Passo 2
ISSOOOO; a força centrípeta! É só igualar então, vem comigo!
Pelo enunciado do problema, o módulo da força normal é igual a duas vezes o módulo da força peso, então a gente fica com:
Fechoooouuu?
Passo 3
Sabemos que a altura é o diametro do círculo, 2R, certo? E lembra que calculamos a velocidade na letra b? Então joga aí!
Fechouuuuu!
Resposta
a)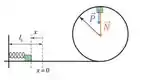 
b)
c)