USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 37d
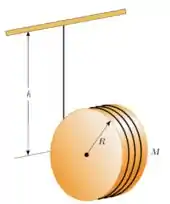
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.
(d) Verifique a resposta anterior utilizando o enfoque da energia.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos um cilindro de raio e massa que é enrolado por um fio e solto para cair devido a ação da gravidade sendo a outra extremidade do fio presa em um lugar fixo.
Com isso queremos descobrir qual é o modulo da velocidade do centro de massa do cilindro quando ele começar a se desenrolar e atinge um comprimento utilizando a ideia de conservação de energia.
Tem ideia do que fazer? 👀
Anteriormente calculamos a aceleração do centro de massa e a velocidade do cilindro a partir da segunda lei de Newton e da equação de Torricelli.
A força de tração e a força gravitacional resulta em uma aceleração de
Já a velocidade foi obtida como
Aplicando a lei da conservação de energia temos que obter o mesmo resultado para .
Bora ver como fazemos isso! 😉
Passo 2
A lei da conservação de energia diz que a energia inicial de um sistema sem perdas é igual a energia final.
Inicialmente o cilindro não possui velocidade, mas possui energia potencial gravitacional, ou seja
Já no instante final o cilindro não possui energia potencial, mas possui energia cinética de translação e de rotação
Podemos reescrever como a relação entre a velocidade tangencial (que é a mesma que a velocidade do centro de massa) e o raio
Substituindo em
Podemos escrever o momento de inercia do cilindro como
Aplicando a conservação de energia fazendo
Simplificando e isolando , chegamos em
O que achou? Foi de boa? Responde aí! 😊
