UFJF – Fisica 1 – Provas - Teste 9 – AV2 SUB – 2015.2 – Questão 4
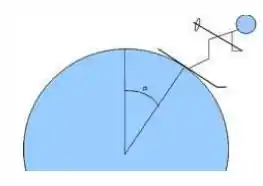
Uma esquiadora parte com velocidade inicial desprezível do topo de uma esfera de neve com raio muito grande e sem atrito, desloca-se diretamente para baixo (figura abaixo). Em que ponto ela perde contato com a esfera e voa seguindo a direção da tangente? Ou seja, no momento em que ela perde contato com a esfera, qual é o ângulo entre vertical e a linha que liga a esquiadora ao centro da esfera de neve?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos mostra uma esquiadora percorrendo uma esfera de neve e, em certo ponto, ela perde o contato.
Queremos descobrir qual o ângulo dessa perda de contato.
Ainda ficou na dúvida? Então bora junto!!
Passo 2
Bom... pelo Teorema da Conservação de Energia, para os pontos inicial e final do sistema, observamos:
Onde é a energia inicial e é a energia final.
Temos:
Passo 3
Por outro lado, pela 2ª Lei de Newton, se fizermos a resultante das forças perpendiculares ao plano da bola de neve e igualando ao produto da massa da esquiadora e sua aceleração radial (única aceleração que atua nesse eixo):
Passo 4
Assim, substituindo as equações encontradas nos Passos 2 e 3, temos:
Entendeu direitinho? Responde aee ;)
