USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 33d
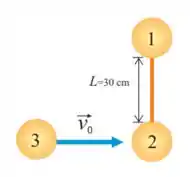
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.
(d) Determine a fração da energia mecânica inicial que é perdida no impacto.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos dois discos de massa presas por uma barra de massa desprezível e comprimento . Um terceiro disco viaja com velocidade em direção ao disco que ao colidirem, se grudam e o sistema inteiro começa a se mover.
Com isso queremos obter a porcentagem de energia que foi dissipada na colisão!
E aí, parece complicado? 👀
Para resolver esse problema, podemos calcular a porcentagem de energia dissipada a partir da relação entre a energia final e a energia inicial do sistema.
Inicialmente, o sistema possui energia cinética de translação. Podemos calcular essa energia como
Já adiantei e escrevi na fórmula pois o único componente que está em movimento é o disco que possui velocidade .
Já após a colisão, a energia é transformada em energia de rotação e em energia cinética de translação como vimos no item anterior que pode ser calculada como
Tranquilo até aqui? 😬
Passo 2
Calculando a energia inicial, vamos obter
Já a energia final é dada por
Pelo teorema dos eixos paralelos e como calculamos anteriormente, a velocidade de translação do centro de massa após a colisão é e a velocidade angular é
Calculando a relação entre e , temos que as perdas é dada por
Fazendo ...
E finalmente, vamos obter
O que achou? Foi de boa? Responde aí! 😊
