Um objeto de massa e dimensões desprezíveis parte do repouso e de uma altura , deslizando por uma rampa suave até encontrar uma superfície horizontal, por onde segue até encontrar uma rampa circular de raio , sobre a qual continua seu movimento (veja a figura). Não há atrito em todo o percurso do objeto, que se dá em um mesmo plano vertical (da figura). Expressando suas respostas em termos dos unitários horizontal e vertical indicados na figura, determine

- O vetor velocidade , nos pontos , e ;
- O vetor de força normal, , nos pontos , e .
Passo 1
Vamos começar escrevendo os dados do problema
Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.
Passo 2
a)
Para acharmos a velocidade em cada ponto devemos ter o seu módulo.
Como não temos forças dissipativas, vulgo força de atrito, ao longo de todo o movimento a energia mecânica se conserva. Além disso, ao longo de todo o movimento as únicas energias presentes são a cinética e a potencial gravitacional.
Então
Passo 3
Vamos achar cada uma dessas energias mecânicas
Isso porque ele é largado do repouso.
Passo 4
Isso porque ele está no chão.
Passo 5
Nesse ponto ele possui altura e velocidade,
Passo 6
Nesse ponto ele possui altura e velocidade,
Passo 7
Vamos igualar a energia em cada ponto com a energia inicial para acharmos a velocidade de cada ponto. Vamos também escrevê-las na forma vetorial, já que é pedido no enunciado.
Começando pelo ponto
A velocidade de é tangente ao movimento, que nos diz que é para direita. Isso quer dizer o que? Que ela é positiva e esta no .
Passo 8
Agora no ponto
A velocidade de é tangente ao movimento, que nos diz que é para cima. Isso quer dizer o que? Que ela é positiva e esta no .
Passo 9
Por fim no ponto
A velocidade de é tangente ao movimento, que nos diz que é para esquerda. Isso quer dizer o que? Que ela é negativa e esta no .
Passo 10
b)
Devemos achar as forças em cada ponto. Como estamos em um movimento circular, devemos ficar atentos a qual força é iguala centrípeta, que será a força ou a soma de forças que aponta para o centro.
No ponto temos

Então
Escrevendo na forma vetorial, como ela aponta para cima
Passo 11
No ponto temos
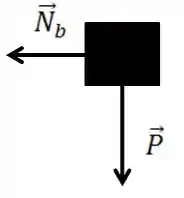
Então
Escrevendo na forma vetorial, como ela aponta para esquerda
Passo 12
No ponto temos
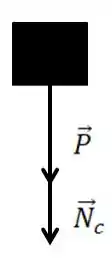
Então
Escrevendo na forma vetorial, como ela aponta para baixo