Um pequeno bloco de massa é liberado em repouso de uma altura acima de uma superfície horizontal. A aceleração da gravidade é . O bloco desliza sem atrito sobre a parte interna de um trilho semicircular de raio . Qual das opções abaixo dá corretamente a rapidez do bloco e o módulo da força normal exercida sobre o bloco quando ele passa pelo ponto mais baixo do trilho?
(A) ;
(B) ;
(C) ;
(D) ;
(E) ;
Passo 1
Para essa situação, como o bloco desliza sem atrito, podemos considerar que há a conservação de energia mecânica no sistema.
Isso é um bom ponto de partida! Podemos relacionar a energia potencial gravitacional com a energia cinética para obter a velocidade do bloco.
Vamos considerar o referencial de energia potencial nula no ponto mais baixo da trajetória:
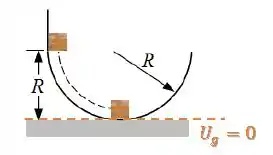
Na situação inicial, o bloco está em repouso, portanto sua energia cinética é zero. Porém, ele se encontra à uma altura , então ele terá energia potencial gravitacional :
Já no segundo instante, o bloco não tem energia potencial gravitacional, porém, ele tem uma energia cinética associada à sua velocidade :
A partir da conservação, temos que:
Achamos que a velcidade no ponto mais baixo do trilho é:
Passo 2
Para achar a força normal, devemos fazer o diagrama de corpo livre no ponto mais baixo do trilho:
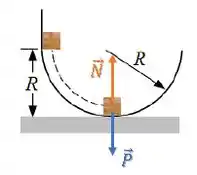
Temos que tomar cuidado para não colocar que as forças peso e normal estão em equilíbrio.
Como o bloco está em uma trajetória circular, existe sobre ele uma força resultante que aponta para o centro do círculo e atua como força centrípeta. Assim:
Substituindo o valor de encontrado, temos:
Ficamos com a alternativa (A).
Resposta
Letra (A)