Um projétil é lançado verticalmente da superfície da Terra com rapidez inicial de . Desprezando-se o atrito com o ar, a que altura acima da superfície da Terra ele chegará?
Dados:
Constante gravitacional:
Raio da Terra:
Massa da Terra:
Passo 1
Temos a velocidade inicial e sabemos como calcular a aceleração da gravidade sofrida pelo corpo, porém como a aceleração é variável conforme a distância, esse problema fica um pouquinho mais chato de se resolver, pois precisamos de uma integral.
Mas, ainda bem que existe um outro caminho...
Vamos pensar no projétil. Se a resistência do ar é desprezível, a única força atuando sobre ele é a força gravitacional com a Terra.
Como a força gravitacional é uma força conservativa (não retira energia do sistema), podemos dizer que a energia mecânica se conserva:
Opa, então é isso mesmo que queremos.

Passo 2
Inicialmente, o projétil está na superfície da Terra e com uma velocidade de .
Então, a energia mecânica inicial será a soma da energia potencial gravitacional com a energia cinética :
Mas qual é a distância ?
A distância do corpo ao centro do planeta quando ele está na superfície é apenas o raio do planeta:
Então:
Passo 3
Já na situação final, o corpo atingiu a altura máxima, ou seja, sua velocidade chegou a zero e ele parou.
Por isso, ele apresenta apresenta apenas uma energia potencial gravitacional , enquanto sua energia cinética é nula:
Mas quem é a distância agora?
A distância é a soma do raio da Terra com a altura a partir da superfície da Terra:
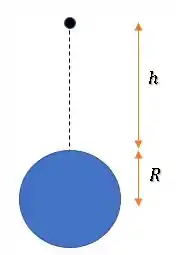
Assim, a energia mecânica final é:
Passo 4
Conservando a energia, temos:
Queremos achar a distância que o projétil alcançou.
Cortando , temos:
Passo 5
Antes de substituir os valores, vamos passar aquela velocidade para a unidade padrão de , afim de facilitar a unidade final:
Então:
Passo 6
Agora, mãos à obra, vamos calcular esse monstro aí:
Vamos calcular cada um dos termos separadamente para não nos enrolarmos.
Aquele numerador fica:
No denominador, temos:
Ainda no denominador, temos também:
Juntando tudo, temos:
Pronto, achamos a distância .
Mas muita calma nessa hora, essa ainda não é a resposta.
Passo 7
Queremos a altura a partir da superfície da Terra:
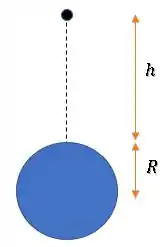
Como a distância é:
Devemos subtrair o raio da Terra dessa distância, para descobrir a altura a partir da superfície: