USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 38
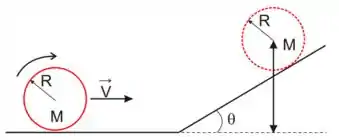
38. Uma roda cilíndrica de raio e massa , rola sem deslizar sobre um plano horizontal, deslocando-se com velocidade , e sobe sobre um plano inclinado de inclinação , continuando a rolar sem deslizamento. Até que altura o centro da roda subirá sobre o plano inclinado?
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nesse problema temos um cilindro de massa e raio que rola sob uma superfície plana horizontal com uma velocidade até começar a subir em um plano inclinado que faz um ângulo com a horizontal.
Com isso queremos descobrir qual é a altura máxima que o centro do cilindro atingirá nessas condições.
Parece complicado, não é? 👀
Nesse caso, temos que aplicar a lei da conservação de energia que nos diz que a energia inicial de um sistema sem perdas é igual a energia final do sistema.
Inicialmente o cilindro possui energia cinética de translação e energia cinética de rotação, ou seja
Já no instante final, quando o cilindro atinge o ponto mais alto do plano inclinado, toda a energia está condensada em energia potencial gravitacional pois não há movimento.
Consideramos a altura pois o centro de massa já estava inicialmente a uma altura e o ganho de altura foi ...
Tranquilo até aqui? 😎
Passo 2
Vamos manipular um pouquinho nossas equações...
Na energia inicial , podemos escrever como a relação entre a velocidade tangencial (a mesma que a velocidade do centro de massa) e o raio
Além disso sabemos que o momento de inercia do cilindro é dado por
Substituindo essas informações em , temos
Igualando a energia inicial à energia final, vamos obter
Simplificando e isolando
Pegou o esquema? Responde Aí! 😁
