USP, Sem Campus, Física 3, Listas de Física 3 - USP - Lista 1 - Lei de Coulomb, Campo Elétrico, Lei de Gauss, Questão 6
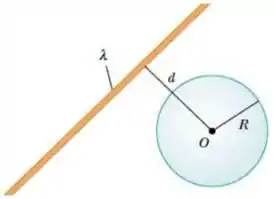
6) Considere um fio muito longo, feito de material isolante e uniformemente carregado com densidade . Obtenha o fluxo do campo elétrico através de uma superfície Gaussiana esférica de raio e centrada no ponto (ver figura), em duas situações: (a) , e (b) .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, temos um fio infinito carregado com densidade e uma superfície gaussiana esférica de raio que está a uma distância do fio. Nosso objetivo é obter o fluxo do campo elétrico nessa superfície caso e caso .
Tem alguma ideia de como fazemos isso? 🤔
Para resolver esse problema, vamos aplicar os conceitos da lei de Gauss para o fluxo elétrico.
Pela lei de Gauss, sabemos que o fluxo elétrico é igual a carga envolvida dividida por .
Então nossa tarefa em ambos os casos é obter a quantidade de carga envolvida pela superfície gaussiana dada no problema.
Sacou? Bora começar! 👀
Passo 2
No item a) a distância do fio até o centro da esfera é maior que o raio da esfera.
Isso quer dizer que o fio não está contido dentro da esfera.
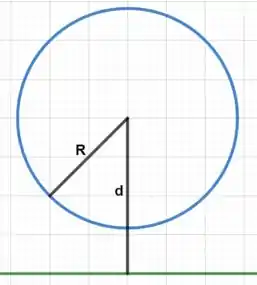
Portanto, a quantidade de carga dentro da esfera é nula, logo, o fluxo elétrico é nulo também
Tranquilo até aqui? 😁
Passo 3
Agora vamos analisar o fluxo sobre a superfície caso , ou seja, a superfície envolve parte do fio...
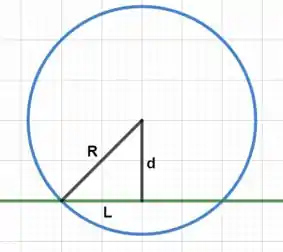
Agora a carga envolvida não é nula e o que temos que fazer é encontrar a quantidade de carga envolvida pela superfície.
Como a densidade de cargas é uniforme, sabemos que
Integrando nos dois lados da equação, vamos obter que a carga envolvida é
Como está definido entre e , temos
Substituindo na lei de Gauss...
Pela figura, vemos que , ou seja
Portanto, o fluxo é dado por
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
